CFA level II – Economics

Learning Module 1: Currency Exchange Rates: Understanding Equilibrium Value

Calculate and interpret the bid–offer spread on a spot or forward currency quotation and describe the factors that affect the bid–offer spread
Identify a triangular arbitrage opportunity and calculate its profit, given the bid–offer quotations for three currencies
Explain spot and forward rates and calculate the forward premium/discount for a given currency
Calculate the mark-to-market value of a forward contract
Explain international parity conditions (covered and uncovered interest rate parity, forward rate parity, purchasing power parity, and the international Fisher effect)
Describe relations among the international parity conditions
Evaluate the use of the current spot rate, the forward rate, purchasing power parity, and uncovered interest parity to forecast future spot exchange rates
Explain approaches to assessing the long-run fair value of an exchange rate
Describe the carry trade and its relation to uncovered interest rate parity and calculate the profit from a carry trade
Explain how flows in the balance of payment accounts affect currency exchange rates
Explain the potential effects of monetary and fiscal policy on exchange rates
Describe objectives of central bank or government intervention and capital controls and describe the effectiveness of intervention and capital controls
Describe warning signs of a currency crisis

What is exchange rate? Forreign exchange market concepts

1.1 Calculate and interpret the bid–offer spread on a spot or forward currency quotation and describe the factors that affect the bid–offer spread

An exchange rate is the price of the base currency expressed in terms of the price currency, or example, a USD/EUR rate of 1.1650 means the euro, the base currency, costs 1.1650 US dollars
Notions: Notation is generally not standardized in global foreign exchange markets, and there are several common ways of expressing the same currency pair (e.g., JPY/ USD, USD:JPY, $/¥). What is common in FX markets, however, is the concept of a “base” and a “price” currency when setting exchange rates. We will sometimes switch to discussing a “domestic” and a “foreign” currency, quoted as foreign/ domestic (f/d). Currency pairs are not described in terms of “foreign” and “domestic” currencies in professional FX markets (may lead confusions).
The spot exchange rate is usually used for settlement on the second business day after the trade date, referred to as T + 2 settlement (the exception being CAD/USD, for which standard spot settlement is T + 1)
Bid-offer price: In foreign exchange markets—as in other financial markets—market participants are presented with a two-sided price in the form of a bid price and an offer price (also called an ask price) quoted by potential counterparties. The bid price is the price, defined in terms of the price currency, at which the counterparty is willing to buy one unit of the base currency. Similarly, the offer price is the price, in terms of the price currency, at which that counterparty is willing to sell one unit of the base currency.
- For example, given a price request from a client, a dealer might quote a two-sided price on the spot USD/EUR exchange rate of 1.1648/1.1652. This means that the dealer is willing to pay USD 1.1648 to buy one EUR and that the dealer is willing to sell one EUR for USD 1.1652.
- The offer price is always higher than the bid price.
- The party in the transaction who requests a two-sided price quote has the option (but not the obligation) to deal at either the bid (to sell the base currency) or the offer (to buy the base currency) quoted by the dealer.
Most currencies, except for the yen, are quoted to four decimal places. The fourth decimal place (0.0001) is referred to as a “pip.” The yen is typically quoted to just two decimal places; in yen quotes, the second decimal place (0.01) is referred to as a pip.

Bid–offer pricing from dealers

The bid–offer spread a dealer provides to most clients typically is slightly wider than the bid–offer spread observed in the interbank market.
For example, if the quote in the interbank USD/EUR spot market is 1.1649/1.1651 (two pips wide), the dealer might quote a client a bid–offer of 1.1648/1.1652 (four pips wide) for a spot USD/EUR transaction. When the dealer buys (sells) the base currency from (to) a client, the dealer is typically expecting to quickly turn around and sell (buy) the base currency in the interbank market.
The size of this spread depends primarily on three factors:
- the bid–offer spread in the interbank foreign exchange market for the two currencies involved.
- the size of the transaction.
  - The size of a transaction can also influence the bid-offer spread given by a dealer. Generally, larger transactions lead to prices further from the current spot exchange rate. For example, a client requesting a spot CAD/USD price for USD 50 million will see a wider spread than one asking for USD 1 million. This wider spread reflects the dealer’s increased difficulty in managing the FX risk in the interbank market.
  - Smaller transactions can also impact the spread. “Retail” quotes, for amounts below 1 million units, including individual trades, often have much larger spreads compared to those in the interbank market.
- the relationship between the dealer and the client.
  - The relationship between the dealer and client can affect the bid-offer spread. Spot FX is often just one of many services the dealer offers, like bond or equity trades. To win more business, the dealer may offer a tighter spread. Dealers may also tighten spreads to get repeat FX business. Credit risk can affect the spread too, with higher risk clients getting wider spreads. However, since spot FX settles quickly (usually in two days), credit risk is less important in deciding the spread.

Bid–offer pricing from interbanks

The size of the bid–offer spread quoted in the interbank market depends on the liquidity in this market.
- The currency pair involved. Liquidity in the major currency pairs—for example, USD/EUR, JPY/USD, and USD/GBP—can be quite high. These markets are almost always deep, with multiple bids and offers from market participants around the world. In other currency pairs, particularly some of the more obscure currency cross rates (e.g., MXN/CHF), market participation is much thinner and consequently the bid–offer spread in the interbank market will be wider.
- The time of day. The interbank FX markets are most liquid when the major FX trading centers are open. Business hours in London and New York—the two largest FX trading centers—overlap from approximately 8:00 a.m. to 11:00 a.m. New York time. and 13:00 to 16:00 London time The interbank FX market for most currency pairs is typically most liquid during these hours.
- Market volatility. As in any financial market, when major market participants have greater uncertainty about the factors influencing market pricing, they will attempt to reduce their risk exposures and/or charge a higher price for taking on risk. In the FX market, this response implies wider bid–offer spreads in both the interbank and broader markets. Geopolitical events (e.g., war, civil strife), market crashes, and major data releases (e.g., US non-farm payrolls) are among the factors that influence spreads and liquidity.

Arbitrage constraints on spot exchange rate quotes

1.2 Identify a triangular arbitrage opportunity and calculate its profit, given the bid–offer quotations for three currencies

Triangular arbitrage

The bid–offer quotes a dealer shows in the interbank FX market must respect two arbitrage constraints; otherwise the dealer creates riskless arbitrage opportunities for other interbank market participants.

First, the bid shown by a dealer in the interbank market cannot be higher than the current interbank offer, and the offer shown by a dealer cannot be lower than the current interbank bid.
Second, the cross-rate bids (offers) posted by a dealer must be lower (higher) than the implied cross-rate offers (bids) available in the interbank market.
- For example, given exchange rate quotes for the currency pairs A/B and C/B, we can back out the implied cross rate of A/C. This implied A/C cross rate must be consistent with the A/B and C/B rates.

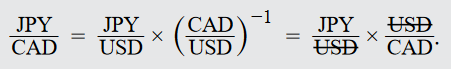
Forward markets

1.3 Explain spot and forward rates and calculate the forward premium/ discount for a given currency

Forwards contracts A

Any exchange rate transaction that has a settlement date longer than T + 2 is a forward contract. Intuition behind forward rate: Investment in risk-free asset should have same return in domestic and foregin countries. Consider an investor with one unit of domestic currency to invest for one year. The investor faces two alternatives:

One alternative is to invest cash for one year at the domestic risk-free rate (i_d). At the end of the year, the investment would be worth (1 + i_d).
The other alternative is to convert the domestic currency to foreign currency at the spot rate of S_f/d and invest for one year at the foreign risk-free rate (i_f). At the end of the period, the investor would have S_f/d(1 + i_f) units of foreign currency. These funds then must be converted back to the investor’s domestic currency. If the exchange rate to be used for this end-of-year conversion is set at the start of the period using a one-year forward contract, then the investor will have eliminated the foreign exchange risk associated with converting at an unknown future spot rate. If we let F_f/d denote the forward rate, the investor would obtain (1/F_f/d) units of the domestic currency for each unit of foreign currency sold forward. Hence, in domestic currency, at the end of the year, the investment would be worth S_f/d(1 + if)(1/F_f/d).

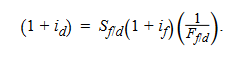
The risk-free assets used in this arbitrage relationship are typically bank deposits quoted using the appropriate Market Reference Rate for each currency involved. The day count convention MRR deposits may be Actual/360 or Actual/365. The main exception to the Actual/360 day count convention is the GBP, for which the convention is Actual/365.

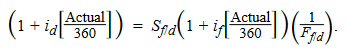
It can be rearranged to:

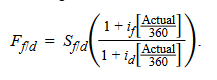
This is covered interest rate parity equation, and it can also be rearranged to give an expression for the forward premium or discount:

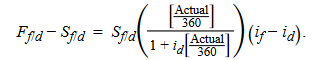
The domestic currency will trade at a forward premium (F_f/d > S_f/d) if, and only if, the foreign risk-free interest rate exceeds the domestic risk-free interest rate (i_f> i_d). It can also be rewrited as

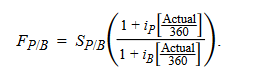
Forwards contracts B: Case of forwards contracts:

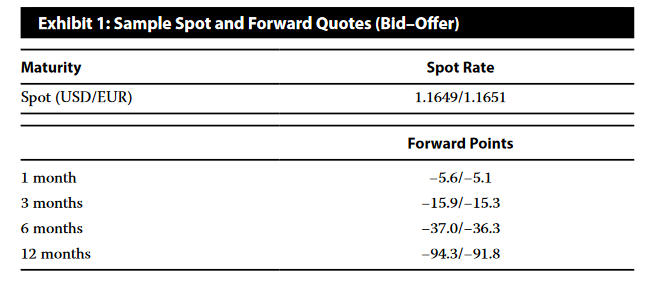
To convert any of these quoted forward points into a forward rate, divide the number of points by 10,000 (to scale it down to the same four decimal places in the USD/ EUR spot quote) and then add the result to the spot exchange rate quote (because the JPY/USD exchange rate is quoted to only two decimal places, forward points for the dollar–yen currency pair are divided by 100).
Be careful, however, about which side of the market (bid or offer) is being quoted. For example, suppose a market participant is selling the EUR forward against the USD and is given a USD/EUR quote. The EUR is the base currency; thus, the market participant must use the bid rates (i.e., hit the bid from interbanks). The three-month forward bid rate in this case would be based on the spot bid and the forward points bid and hence would be

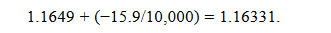
The market participant would be selling EUR three months forward at a price of USD 1.16331 per EUR.

The mark-to-market value of a forward contract

1.4 Calculate the mark-to-market value of a forward contract

Forwards contracts C: Mark-to-market value of forward contract

Suppose that a market participant bought GBP 10 million for delivery against the AUD in six months at an “all-in” forward rate of 1.8100 AUD/ GBP. Assume the bid–offer quotes for spot and forward points three months prior to the settlement date are as follows:

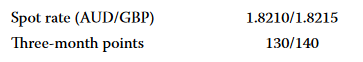
To sell GBP (the base currency in the AUD/GBP quote), we will be calculating the bid side of the market. Hence, the appropriate all-in three-month forward rate to use is 1.8210 + 130/10,000 = 1.8340. This means that the market participant originally bought GBP 10 million at an AUD/ GBP rate of 1.8100 and subsequently sold that amount at a rate of 1.8340. These GBP amounts will net to zero at the settlement date (GBP 10 million both bought and sold), but the AUD amounts will not, because the forward rate has changed. The AUD cash flow at the settlement date will be (1.8340 − 1.8100) × 10,000,000 = +AUD 240,000. Suppose that three-month AUD MRR is 2.40% (annualized).

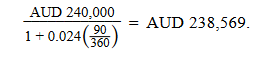
This result is the mark-to-market value of the original long GBP 10 million six-month forward when it is closed out three months prior to settlement.

Summary:

Create an offsetting forward position: Match the original forward position (e.g., sell GBP 10 million if originally long GBP 10 million).
Determine the all-in forward rate: Use the bid/offer side depending on whether the base currency is being sold/bought.
Calculate the settlement day cash flow: Multiply the contract size by the difference between the original and new forward rates. If the originally long (short) currency appreciates (depreciates), there will be a cash inflow (outflow).
Calculate the present value of the cash flow: Discount the cash flow at the future settlement date using a rate that matches the currency of the cash flow (the country whose currency is being held).

The factors that affect the bid–offer spread for forward points are the same as those we discussed for spot bid–offer rates: the interbank market liquidity of the underlying currency pair, the size of the transaction, and the relationship between the client and the dealer. For forward bid–offer spreads, we can also add a fourth factor: the term of the forward contract. Generally, the longer the term of the forward contract, the wider the bid–offer spread.

International Parity Conditions

1.5 Explain international parity conditions (covered and uncovered interest rate parity, forward rate parity, purchasing power parity, and the international Fisher effect)

The key international parity conditions are as follows:
- 1. covered interest rate parity
- 2. uncovered interest rate parity
- 3. forward rate parity
- 4. purchasing power parity
- 5. the international Fisher effect.

Covered and uncovered interest rate parityand forward rate parity

1.6 Explain international parity conditions (covered and uncovered interest rate parity, forward rate parity, purchasing power parity, and the international Fisher effect)

1.7 Describe relations among the international parity conditions

1.8 Evaluate the use of the current spot rate, the forward rate, purchasing power parity, and uncovered interest parity to forecast future spot exchange rates

Covered interest rate parity

We have already discussed covered interest rate parity in our examination of forward exchange rates. Under this parity condition, an investment in a foreign money market instrument that is completely hedged against exchange rate risk should yield exactly the same return as an otherwise identical domestic money market investment.

Uncovered interest rate parity

根据 UIP 理论，较高的利率通常伴随着汇率的预期贬值。也就是说，如果一个国家的利率比另一个国家高，虽然投资者可以获得更高的利息收入，但汇率在未来的贬值预期将抵消这部分收益。例如，如果一个国家的利率高出 2%，那么其货币可能会预期贬值 2%，使得投资者的总收益率与低利率国家的收益率相同。假设不发生这种贬值，那么投资者就会持续向高利率国家投资，从而无风险地获得比低利率国家更高的回报。这种套利机会在有效市场中应当不存在，汇率的调整（贬值）会确保不同国家的投资收益率一致。
UIP 建立在无套利的基础上。如果高利率国家的货币不贬值，投资者可以简单地借入低利率国家的货币，兑换为高利率国家的货币，并获得无风险的高回报。这种套利行为会导致大量资金流入高利率国家，并推高该国货币的汇率。然而，市场通过汇率调整来消除套利机会，这就是为什么 UIP 预测高利率国家的货币会贬值，而不是升值。
利率高的国家往往反映出该国经济中存在较大的风险（如通胀上升、经济不确定性增加等），因此投资者需要更高的利率作为补偿。这种经济风险可能会让投资者预期该国的货币在未来贬值，从而影响资本流动。此外，利率较高的国家可能是因为经济不稳定或通胀压力较大，这使得该国货币的购买力在未来降低。投资者虽然能够在短期内获得较高的利率回报，但长期来看，汇率贬值可能会让投资者失去通过高利率获得的收益。
短期效应：在利率上升的初期，确实可能会吸引资本流入高利率国家，导致货币短期升值。高利率带来高收益率吸引力，资金流入可能在短期内推动货币升值。长期效应：随着时间推移，市场开始意识到利率差异的背后因素（如通胀、经济不确定性），因此预期该国货币会贬值。汇率逐渐调整，以确保不同国家的收益率差异被汇率变化所抵消。
虽然 UIP 是理论上的无套利条件，但在现实中，UIP 经常在短期内未必成立。实际上，高利率货币经常在短期内升值，而不是贬值，这一现象被称为前向溢价之谜（forward premium puzzle）。这意味着投资者在短期内可能通过持有高利率货币获得更高的收益。但在长期，随着汇率预期的调整，汇率贬值通常会弥补利率差异。

According to the uncovered interest rate parity condition, the expected return on an uncovered (i.e., unhedged) foreign currency investment should equal the return on a comparable domestic currency investment. Uncovered interest rate parity states that the change in spot rate over the investment horizon should, on average, equal the differential in interest rates between the two countries. That is, the expected appreciation/depreciation of the exchange rate will just offset the yield differential.

In domestic currency terms, the investment return on an uncovered (or unhedged) foreign-currency-denominated investment is equal to (1 + i_f)(1 − %Δ S_f/d) − 1. This return can be approximated by ≅ i_f− % Δ S_f/d. That is %Δ S^e_f/d = i_f− i_d

The arbitrage condition that underlies covered interest rate parity (illustrated earlier) can be rearranged to give an expression for the forward premium or discount:

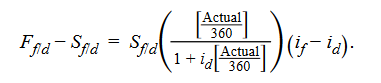
The domestic currency will trade at a forward premium (F_f/d > S_f/d) if, and only if, the foreign risk-free interest rate exceeds the domestic risk-free interest rate (i_f > i_d). For the sake of simplicity, we assume that the investment horizon is one year, so that

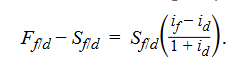
Because the 1 + i_d denominator will be close to 1, we can approximate the above equation as follows:

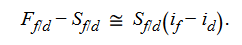
This covered interest rate parity equation can be rearranged to show the forward discount or premium as a percentage of the spot rate:

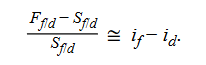
We have also shown that if uncovered interest rate parity holds, then the expected change in the spot rate is equal to the interest rate differential:

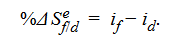
We can link the covered interest rate parity and uncovered interest rate parity equations as follows:

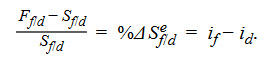
The following equation is Uncovered interest rate parity:

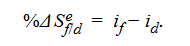
Thus, the forward premium (discount) on a currency, expressed in percentage terms, equals the expected percentage appreciation (depreciation) of the domestic currency (assuming that the uncovered interest rate parity condition holds).

In theory, then, the forward exchange rate will be an unbiased forecast of the future spot exchange rate if both covered and uncovered interest rate parity hold:

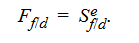
This condition is often referred to as forward rate parity.

Purchasing power parity

1.6 Explain international parity conditions (covered and uncovered interest rate parity, forward rate parity, purchasing power parity, and the international Fisher effect)

1.7 Describe relations among the international parity conditions

1.8 Evaluate the use of the current spot rate, the forward rate, purchasing power parity, and uncovered interest parity to forecast future spot exchange rates

PPP is the relationship between exchange rates and inflation differentials.
According to the law of one price, identical goods should trade at the same price across countries when valued in terms of a common currency. The law of one price asserts that the foreign price of good x, P^x_f, should equal the exchange rate–adjusted price of the identical good in the domestic country, P^x_d:

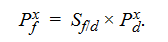
The absolute version of PPP simply extends the law of one price to the broad range of goods and services that are consumed in different countries. The broad price level of the foreign country (P_f) should equal the currency-adjusted broad price level in the domestic country (P_d)

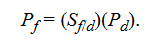
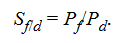
According to the relative version of PPP, the percentage change in the spot exchange rate (%ΔS_f/d) will be completely determined by the difference between the foreign and domestic inflation rates (π_f − π_d):

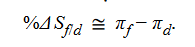
Whereas the relative version of PPP focuses on actual changes in exchange rates being driven by actual differences in national inflation rates, the ex ante version of PPP asserts that the expected changes in the spot exchange rate are entirely driven by expected differences in national inflation rates. Ex ante PPP can be expressed as:

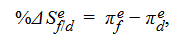
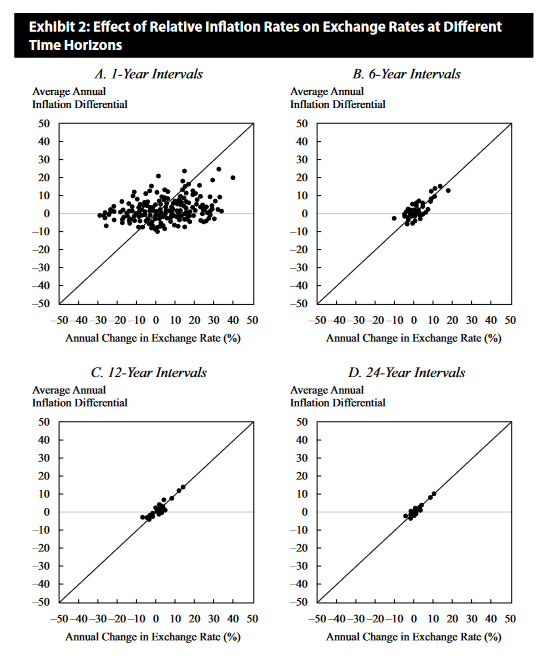
Studies have found that while over shorter horizons nominal exchange rate movements may appear random, over longer time horizons nominal exchange rates tend to gravitate toward their long-run PPP equilibrium values.

Fisher effect, real interest rate parity, and international Fisher effect

1.6 Explain international parity conditions (covered and uncovered interest rate parity, forward rate parity, purchasing power parity, and the international Fisher effect)

1.7 Describe relations among the international parity conditions

1.8 Evaluate the use of the current spot rate, the forward rate, purchasing power parity, and uncovered interest parity to forecast future spot exchange rates

1.9 Explain approaches to assessing the long-run fair value of an exchange rate

According to what economists call the Fisher effect, one can break down the nominal interest rate (i) in a given country into two parts: (1) the real interest rate (r) in that particular country and (2) the expected inflation rate (π_e) in that country: i = r + π_e

To relate this concept to exchange rates, we can write the Fisher equation for both the domestic country and a foreign country. If the Fisher effect holds, the nominal interest rates in both countries will equal the sum of their respective real interest rates and expected inflation rates:

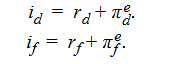
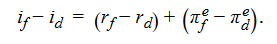
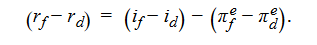
To tie this material to our previous work on exchange rates, recall our expression for uncovered interest rate parity:

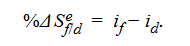
Recall also the expression for ex ante PPP:

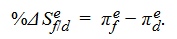
The difference in expected inflation rates equals the expected change in the exchange rate. Combining these two expressions, we derive the following:

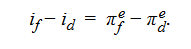
The nominal interest rate spread is equal to the difference in expected inflation rates. We can therefore conclude that if uncovered interest rate parity and ex ante PPP hold,

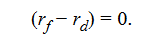
The above proposition that real interest rates will converge to the same level across different markets is known as the real interest rate parity condition.

Finally, if real interest rates are equal across markets, then it also follows that the foreign–domestic nominal yield spread is determined solely by the foreign–domestic expected inflation differential:

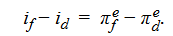
This is known as the international Fisher effect. The reader should be aware that some authors refer to uncovered interest rate parity as the “international Fisher effect.”

Summing up

1. According to covered interest rate parity, arbitrage ensures that nominal interest rate spreads equal the percentage forward premium (or discount).
2. According to uncovered interest rate parity, the expected percentage change of the spot exchange rate should, on average, be reflected in the nominal interest rate spread.
3. If both covered and uncovered interest rate parity hold—that is, the nominal yield spread equals both the forward premium (or discount) and the expected percentage change in the spot exchange rate—then the forward exchange rate will be an unbiased predictor of the future spot exchange rate.
4. According to the ex ante PPP approach to exchange rate determination, the expected change in the spot exchange rate should equal the expected difference between domestic and foreign inflation rates.
5. Assuming the Fisher effect holds in all markets—that is, the nominal interest rate in each market equals the real interest rate plus the expected inflation rate—and also assuming that real interest rates are broadly the same across all markets (real interest rate parity), then the nominal yield spread between domestic and foreign markets will equal the domestic–foreign expected inflation differential, which is the international Fisher effect.
6. If ex ante PPP and the international Fisher effect hold, then expected inflation differentials should equal both the expected change in the exchange rate and the nominal interest rate differential. This relationship implies that the expected change in the exchange rate equals the nominal interest rate differential, which is uncovered interest rate parity.

In sum, if all the key international parity conditions held at all times, then the expected percentage change in the spot exchange rate would equal:

the forward premium or discount (expressed in percentage terms) (both covered and uncovered interest rate parity)
the nominal yield spread between countries (uncovered interest rate parity)
the difference between expected national inflation rates (ex ante PPP)

Carry trade

1.10 Describe the carry trade and its relation to uncovered interest rate parity and calculate the profit from a carry trade

Uncovered interest rate parity is one of the most widely tested propositions in international finance. The evidence suggests that uncovered interest rate parity does not hold over short and medium time periods. Studies have generally found that high-yield currencies, on average, have not depreciated and low-yield currencies have not appreciated to the levels predicted by interest rate differentials. These findings underscore the potential profitability of a trading strategy known as the FX carry trade, which involves taking long positions in high-yield currencies and short positions in low-yield currencies.

Carry trades are leveraged trades (borrow in the funding currency, invest in the high-yield currency), and leverage increases the volatility in the investor’s return on equity.
Example: Canadian dollars at 1% and earn 9% on an investment in Brazilian reals for one year. To execute the trade to earn 8% from the interest rate differential, the trader will do the following:
- 1. Borrow Canadian dollars at t = 0.
- 2. Sell the dollars and buy Brazilian reals at the spot rate at t = 0.
- 3. Invest in a real-denominated investment at t = 0.
- 4. Liquidate the Brazilian investment at t = 1.
- 5. Sell the reals and buy dollars at the spot rate at t = 1. 6. Pay back the dollar loan.
During periods of low volatility, carry trades tend to generate positive returns, but they are prone to significant crash risk in turbulent times. Although carry trades have generated positive returns on average in the past, the negative skew and fat tails indicate that carry trades have tended to have more frequent and larger losses than would have been experienced had the return distribution been normal.

The impact of balance of payments flows

1.11 Explain how flows in the balance of payment accounts affect currency exchange rates

Effects of current account imbalances on exchange rates
Effects of capital flows
A country’s balance of payments consists of its current account as well as its capital and financial account.

Current Account Imbalances and the Determination of Exchange Rates

The flow supply/demand channel
- countries with persistent current account surpluses should see their currencies appreciate over time, and countries with persistent current account deficits should see their currencies depreciate over time.
The portfolio balance channel
- Current account imbalances shift financial wealth from deficit nations to surplus nations. Countries with trade deficits will finance their trade with increased borrowing. This behavior may lead to shifts in global asset preferences, which in turn could influence the path of exchange rates.
- For example, nations running large current account surpluses versus the United States might find that their holdings of US dollar–denominated assets exceed the amount they desire to hold in a portfolio context. Actions they might take to reduce their dollar holdings to desired levels could then have a profound negative impact on the dollar’s value.
- 经常账户失衡将金融财富从赤字国转移到盈余国。贸易赤字国通过增加借贷来融资，这可能导致全球资产偏好的转变，进而影响汇率。
- 例如，与美国有大量经常账户盈余的国家，可能发现其持有的美元资产超过其投资组合所需。为将美元持有量降至理想水平，他们的减持行动可能对美元价值产生深远的负面影响。
The debt sustainability channel
- The third mechanism through which current account imbalances can affect exchange rates is the so-called debt sustainability channel. According to this mechanism, there should be some upper limit on the ability of countries to run persistently large current account deficits. If a country runs a large and persistent current account deficit over time, eventually it will experience an untenable rise in debt owed to foreign investors. If such investors believe that the deficit country’s external debt is rising to unsustainable levels, they are likely to reason that a major depreciation of the deficit country’s currency will be required at some point to ensure that the current account deficit narrows significantly and that the external debt stabilizes at a level deemed sustainable.
- The existence of persistent current account imbalances will tend to alter the market’s notion of what exchange rate level represents the true, long-run equilibrium value. For deficit nations, ever-rising net external debt levels as a percentage of GDP should give rise to steady (but not necessarily smooth) downward revisions in market expectations of the currency’s long-run equilibrium value. For surplus countries, ever-rising net external asset levels as a percentage of GDP should give rise to steady upward revisions of the currency’s long-run equilibrium value. Hence, one would expect currency values to move broadly in line with trends in debt and/or asset accumulation.
- 经常账户失衡通过债务可持续性渠道影响汇率：当一国长期存在大量经常账户赤字时，其对外债务将不可持续地上升。若投资者认为该国外债达到了不可持续的水平，他们可能预期该国货币需要大幅贬值，以缩小经常账户赤字并使外债稳定在可持续水平。
- 持续的经常账户失衡会改变市场对汇率长期均衡值的认知。对于赤字国，净外债占GDP比例不断上升，会引发市场对其货币长期均衡价值的持续下调；对于盈余国，净外部资产占GDP比例不断上升，则会引发市场对其货币长期均衡价值的持续上调。因此，货币价值往往与债务或资产积累的趋势大致一致。

Capital flow

1.12 Explain how flows in the balance of payment accounts affect currency exchange rates

Governments in emerging markets often resist currency appreciation from excessive capital inflows by using capital controls or selling their currency in the FX market.
Sometimes, capital flows due to interest rate spreads have little impact on the trend in exchange rates.
高收益、易通胀的新兴市场国家通过逐步提高国内利率来收紧货币政策，降低通胀预期。持续的高名义收益率差和通胀预期的下降对高收益货币的价值产生上行压力，长期带来套利交易利润。High-yield, inflation-prone emerging market countries tighten monetary policy by gradually raising domestic interest rates to lower inflation expectations. Sustained high nominal yield spreads and declining inflation expectations create upward pressure on the high-yield currency, leading to long-term carry trade profits.
政策制定者实施吸引外国投资的政策，如更紧的财政政策、金融市场自由化、减少资本流动限制、私有化和改善营商环境。这些政策使投资者降低持有高收益货币资产的风险溢价，并上调对该国货币长期均衡价值的评估。Policymakers implement policies to attract foreign investment, such as tighter fiscal policies, financial market liberalization, reducing capital flow restrictions, privatization, and improving the business environment. These policies lower the risk premium for holding high-yield currency assets and lead investors to revise upward the currency’s long-run equilibrium value.
名义利率差对汇率的影响是渐进的，因为货币政策调整和通胀预期、风险溢价的变化都需要时间。这些因素相互强化，可能导致资本流动和套利交易回报的持续存在。The impact of nominal interest rate spreads on exchange rates is gradual, as monetary policy adjustments and changes in inflation expectations and risk premiums take time. These factors reinforce each other, leading to persistent capital flows and carry trade returns over time.
Increasing equity prices can also attract foreign capital. Although exchange rates and equity market returns sometimes exhibit positive correlation, the relationship between equity market performance and exchange rates is not stable. Such instability in the correlation between exchange rates and equity markets makes it difficult to form judgments on possible future currency moves based solely on expected equity market performance. Correlations between equity returns and exchange rates are unstable in the short term and tend toward zero in the long run.

Greater financial integration of the world’s capital markets and greater freedom of capital to flow across national borders have increased the importance of global financial flows in determining exchange rates, interest rates, and broad asset price trends. One can cite many examples in which global financial flows either caused or contributed to extremes in exchange rates, interest rates, or asset prices.

In numerous cases, global capital flows have helped fuel boom-like conditions in emerging market economies for a while before, suddenly and often without adequate warning, those flows reversed. The reversals often caused a major economic downturn, sovereign default, a serious banking crisis, and/or significant currency depreciation. Excessive emerging market capital inflows often plant the seeds of a crisis by contributing to:

1. an unwarranted appreciation of the emerging market currency,
2. a huge buildup in external indebtedness,
3. an asset bubble,
4. a consumption binge that contributes to explosive growth in domestic credit and/or the current account deficit, or
5. an overinvestment in risky projects and questionable activities.

Monetary and FIscal policies

1.13 Explain the potential effects of monetary and fiscal policy on exchange rates

The Mundell–Fleming Model

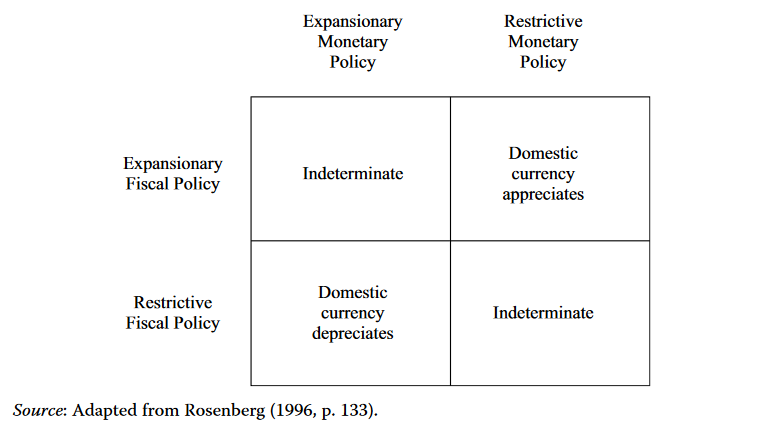
Expansionary monetary policy affects growth, in part, by reducing interest rates and thereby increasing investment and consumption spending. Given flexible exchange rates and expansionary monetary policy, downward pressure on domestic interest rates will induce capital to flow to higher-yielding markets, putting downward pressure on the domestic currency. The more responsive capital flows are to interest rate differentials, the greater the depreciation of the currency.
Expansionary fiscal policy either directly through increased spending or indirectly via lower taxes—typically exerts upward pressure on interest rates because larger budget deficits must be financed. With flexible exchange rates and mobile capital, the rising domestic interest rates will attract capital from lower-yielding markets, putting upward pressure on the domestic currency.

One of the major shortcomings of the pure monetary approach is the assumption that purchasing power parity holds in both the short and long runs. Because purchasing power parity rarely holds in either the short or medium run, the pure monetary model may not provide a realistic explanation of the impact of monetary forces on the exchange rate.

Monetary Models of Exchange Rate Determination

To rectify that problem, Dornbusch (1976) constructed a modified monetary model that assumes prices have limited flexibility in the short run but are fully flexible in the long run.
Long-Run Outcome: An increase in the domestic money supply causes domestic prices to rise proportionally, leading to a depreciation of the currency in line with the pure monetary model.
Short-Run Dynamics with Sticky Prices: If prices are sticky in the short run, an increase in the money supply lowers interest rates, causing capital outflows and a depreciation of the currency that overshoots its long-run equilibrium value.
Return to Equilibrium: Over time, as prices and interest rates adjust, the currency appreciates back toward its long-run equilibrium exchange rate as predicted by the monetary model.

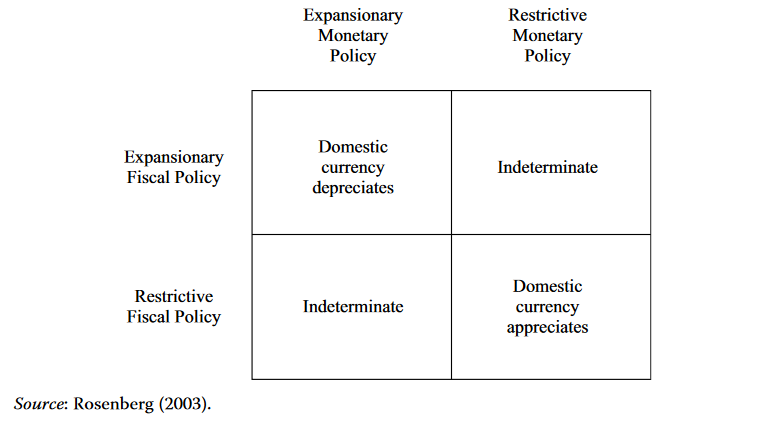
The Portfolio Balance Approach

The Mundell–Fleming model is essentially a short-run model of exchange rate determination. It makes no allowance for the long-term effects of budgetary imbalances that typically arise from sustained fiscal policy actions. The portfolio balance approach to exchange rate determination remedies this limitation. In our previous discussion of the portfolio balance channel, we stated that the currencies of countries with trade deficits will decline over time. We expand that discussion here to more closely examine how exchange rates change over the long term.
The portfolio balance approach explains how sustained government budget deficits influence exchange rates through investors’ portfolio adjustments. While expansionary fiscal policy may strengthen a currency in the short run by attracting foreign investment, over time, the accumulation of debt can lead to concerns about debt financing and sustainability. These concerns may cause investors to demand higher returns or anticipate currency depreciation, ultimately leading to a decline in the currency’s value. Integrating this approach with the Mundell–Fleming model provides a comprehensive understanding of the short-term and long-term effects of fiscal policy on exchange rates in an environment with high capital mobility.

Exchange rate management: intervention and controls

1.14 Describe objectives of central bank or government intervention and capital controls and describe the effectiveness of intervention and capital controls

Capital flows can be both a blessing and a curse. Capital inflows can be a blessing when they increase domestic investment, thereby increasing a country’s economic growth and asset values. Currency appreciation often follows, which increases returns to global investors. Capital inflows can be a curse, however, if they fuel boom-like conditions, asset price bubbles, and overvaluation of a country’s currency. If capital inflows then reverse, the result may be a major economic downturn, a significant decline in asset prices, and a large depreciation of the currency. Capital inflows often are driven by a combination of “pull” and “push” factors. Pull factors represent a favorable set of developments that encourage foreign capital inflows. These factors may stem from both the public and private sectors. Examples of better economic management by a government include:

a decrease in inflation and inflation volatility,
more-flexible exchange rate regimes,
improved fiscal positions,
privatization of state-owned entities,
liberalization of financial markets, and
lifting of foreign exchange regulations and controls.

the key issue for policymakers is whether intervention and capital controls will actually work in terms of

(1) preventing currencies from appreciating too strongly,
(2) reducing the aggregate volume of capital inflows, and
(3) enabling monetary authorities to pursue independent monetary policies without having to worry about whether changes in policy rates might attract too much capital from overseas.

Warning signs of currency crisis

1.15 Describe warning signs of a currency crisis

Because most crisis episodes have not been adequately anticipated, a great deal of effort has been spent developing early warning systems. One of the problems in developing an early warning system is that views on the underlying causes of currency crises differ greatly. One school of thought contends that currency crises tend to be precipitated by deteriorating economic fundamentals, while a second school contends that currency crises can occur out of the blue, with little evidence of deteriorating fundamentals preceding them.

If, according to the first school of thought, deteriorating economic fundamentals often precede crises and if those economic fundamentals tend to deteriorate steadily and predictably, then it should be possible to construct an early warning system to anticipate when a currency might be vulnerable.
The second school of thought argues that, although evidence of deteriorating economic fundamentals might explain a relatively large number of currency collapses, there might be cases in which economies with relatively sound fundamentals have their currencies come under attack. Clearly, these currency crises would be more difficult to predict. Events that are largely unrelated to domestic economic fundamentals include sudden adverse shifts in market sentiment that become self-fulfilling prophecies and contagion from crises in other markets. A crisis may spread to a country when, for example, the country devalues its currency to keep its exports competitive with those of another country that devalued.

Although the variables and methodologies differ from one study to the next, the following conditions were identified in one or more studies:

1. Prior to a currency crisis, the capital markets have been liberalized to allow the free flow of capital.
2. There are large inflows of foreign capital (relative to GDP) in the period leading up to a crisis, with short-term funding denominated in a foreign currency being particularly problematic.
3. Currency crises are often preceded by (and often coincide with) banking crises.
4. Countries with fixed or partially fixed exchange rates are more susceptible to currency crises than countries with floating exchange rates.
5. Foreign exchange reserves tend to decline precipitously as a crisis approaches.
6. In the period leading up to a crisis, the currency has risen substantially relative to its historical mean.
7. The ratio of exports to imports (known as “the terms of trade”) often deteriorates before a crisis.
8. Broad money growth and the ratio of M2 (a measure of money supply) to bank reserves tend to rise prior to a crisis.
9. Inflation tends to be significantly higher in pre-crisis periods compared with tranquil periods.

These factors are usually interrelated and often feed off one another. For example, in the case of the first five factors, large inflows of foreign capital occur because the financial markets have been liberalized and domestic banks have borrowed abroad. If the borrowing is denominated in a foreign currency and the domestic currency initially depreciates, the bank may have trouble servicing its debt, especially when the debt is of shorter maturity. This scenario may cause foreign investors to withdraw capital and speculators to short the currency, with their actions causing further declines in the currency. If the government is trying to maintain the currency’s value, it could increase interest rates to stem capital outflows or defend its currency using direct intervention. The former action may worsen the banking industry’s condition and slow down the economy. In the latter approach, the government will have to spend down its foreign currency reserves to buy its own currency in the foreign exchange markets. If the government appears unwilling or unable to defend its currency, then capital outflows and speculative attacks will increase. The fifth through seventh factors are related because an overvalued currency may make the country’s exports less competitive. With fewer exports, the country is not able to earn as much foreign currency. Other interrelationships occur because these factors often coincide.

Models cannot predict every crisis, and they sometimes generate false alarms. Nevertheless, an early warning system can be useful in assessing and preparing for potential negative tail risks. As with any analytical tool, the implementation of an early warning system requires integration with other analysis and judgment that cannot be easily quantified or conceptualized.

Learning Module 2: Economic Growth

Compare factors favoring and limiting economic growth in developed and developing economies
Describe the relation between the long-run rate of stock market appreciation and the sustainable growth rate of the economy
Explain why potential GDP and its growth rate matter for equity and fixed income investors
Contrast capital deepening investment and technological progress and explain how each affects economic growth and labor productivity
Demonstrate forecasting potential GDP based on growth accounting relations
Explain how natural resources affect economic growth and evaluate the argument that limited availability of natural resources constrains economic growth
Explain how demographics, immigration, and labor force participation affect the rate and sustainability of economic growth
Explain how investment in physical capital, human capital, and technological development affects economic growth
Compare classical growth theory, neoclassical growth theory, and endogenous growth theory
Explain and evaluate convergence hypotheses
Describe the economic rationale for governments to provide incentives to private investment in technology and knowledge
Describe the expected impact of removing trade barriers on capital investment and profits, employment and wages, and growth in the economies involved

GDP and per capita GDP are the best indicators economists have for measuring a country’s standard of living and its level of economic development. Economic growth is calculated as the annual percentage change in real GDP or in real per capita GDP. Growth in real GDP measures how rapidly the total economy is expanding. Real per capita GDP reflects the average standard of living in each countryessentially the average level of material well-being. Growth in real GDP per capita (i.e., real GDP growing faster than the population) implies a rising standard of living.

Factors favoring and limiting economic growth in developed and developing economies

2.1 Compare factors favoring and limiting economic growth in developed and developing economies

Savings and Investment
- A country amasses capital from both private and public sector investments. It is noteworthy that Investments are usually made from savings. Increasing the investment rate in developing countries is difficult because there is a lower disposable income for meaningful savings than in developed countries.
Financial Markets and Intermediaries
- Any financial market (such as banks)’s function is to direct savers’ funds toward viable projects leading to economic growth. The financial market achieves this by:
  1. Filtering those seeking funding while supervising those who have acquired funds to ensure that they indulge in projects that generate risk-adjusted returns.Promote savings and risk-taking by constructing viable investment instruments.Reduction of credit blocks that companies must surmount in financing capital investments.
  If a financial market fails its mandate, a decline in credit standards and increasing leverage will attract risk, undermining growth.
Political Stability, Rule of Law, and Property Rights
- Property rights are legal structures that protect private and intellectual property. In developed countries, the legal system is well established to protect these rights. The same might not be said about most developing countries.Political instability occasioned by such occurrences as war increases investment risk and cripples foreign investment and economic growth. Political instability is much more experienced in developing countries than in developed countries.
Education and Health Care Systems
- In most developing countries, the education system has not been well established compared with developed countries. Therefore, a large portion of the labor force is illiterate, with a small portion having the capacity to use the ever-changing technology. Moreover, there exists a brain drain in developing countries. Highly skilled citizens leave their developing countries for developed countries, further depriving their countries of the expertise they need for development. Therefore, improving the education system through formal schooling and informal job training works best for the economy.Due to the unavailability of top-grade health amenities in developing countries, the life expectancy in such countries is lower than in developed countries. For instance, diseases are more prevalent in African countries, worsened by the HIV/AIDS epidemic.
Free Trade and Unrestricted Capital Flows
- An open economy is where capital and trade flow freely. Since foreign investment is a source of funds, it can increase income, savings, and investments. Therefore, developing countries would benefit from the formulation of policies that attract external investment. Such policies include the removal of higher trade tariffs on imports and easing restrictions on all foreign investments. On the other hand, free trade boosts a country’s economy by availing more goods and services at lower prices.
Tax and Regulatory Systems
- Limited tax regulations catalyze business activities and the entry of new companies into a market, thus increasing the productivity levels of a country. In most developing countries, a tax regulatory system discourages foreign investors, worsening the state of their economy.

Developing countries differ significantly from developed countries in terms of their institutional structure and their legal and political environments. Lack of appropriate institutions and poor legal and political environments restrain growth in the developing economies and partially explain why these countries are poor and experience slow growth. Factors limiting growth include the following:

Low rates of saving and investment
Poorly developed financial markets
Weak, or even corrupt, legal systems and failure to enforce laws
Lack of property rights and political instability
Poor public education and health services
Tax and regulatory policies discouraging entrepreneurship
Restrictions on international trade and flows of capital
In addition to these institutional restraints, as we will see later, growth in developing countries may be limited by a lack of physical, human, and public capital, as well as little or no innovation.

Why potential growth matters to investors

2.2 Describe the relation between the long-run rate of stock market appreciation and the sustainable growth rate of the economy

2.3 Explain why potential GDP and its growth rate matter for equity and fixed income investors

The impact on equity market

Grinold-Kroner (2002) decomposition of the return to equity (ROE)

Over time, the dividend yield (dy) has remained relatively stable and serves as a significant contributor to equity market returns. The repricing term, Δ(P/E), reflects changes in P/E ratios. Higher GDP growth rates often correlate with rising P/E ratios, as investors view the economy as less risky and are willing to pay more for earnings. However, the main impact of this term is the volatility of P/E ratios throughout market cycles.
Earnings growth per share, influenced by inflation, real economic growth, and changes in shares traded, is the key channel through which economic growth affects equity returns. When the number of shares remains constant, real economic growth leads to higher equity returns. However, empirical evidence on the direct link between economic growth and equity returns is mixed, suggesting that the dilution effect, represented by ΔS (change in shares outstanding), is crucial in determining expected returns. This dilution varies across countries due to factors like economic development and financial market sophistication.
The divergence between economic growth and equity returns arises for two reasons. First, publicly traded companies either buy back shares, increasing returns by reducing shares outstanding, or issue new shares, diluting returns. The net buybacks (nbb) capture the balance between these activities at the national level. Second, a portion of economic growth stems from small- and medium-sized firms not publicly traded, leading to a divergence between overall economic growth and earnings growth of listed companies. This is known as the relative dynamism of the economy (rd). Therefore, the ΔS dilution effect reflects both net buybacks and the impact of unlisted firms.

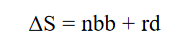
The impact on fixed-income

A higher rate of potential GDP growth improves the general credit quality of fixed-income securities. Credit rating agencies use the growth rate of potential GDP in evaluating the credit risk of sovereign debt. All else equal, slower estimated potential GDP growth raises the perceived risk of these bonds.
Monetary policy decisions are affected by the difference between an economy’s estimated potential output and its actual operating level (referred to as the output gap) and by the growth of actual GDP relative to the long-term sustainable growth rate. Thus, fixed-income investors need to closely monitor the output gap and growth rates of actual and potential GDP to assess the likelihood of a change in central bank policy.
Government budget deficits typically increase during recessions and decrease during expansions. In examining fiscal policy, actual fiscal positions are often judged relative to structural or cyclically adjusted deficits, a theoretical budgetary balance that would exist if the economy were operating at its potential GDP.

Production function and growth accounting

2.4 Contrast capital deepening investment and technological progress and explain how each affects economic growth and labor productivity

2.5 Demonstrate forecasting potential GDP based on growth accounting relations

Production Function

A production function is a model of the quantitative link between the inputs (factors of production), technology, and output. A two-factor aggregate production function with labor and capital as the inputs can be represented as

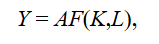
where Y denotes the level of aggregate output in the economy, L is the quantity of labor or number of workers or hours worked in the economy, and K is an estimate of the capital services provided by the stock of equipment and structures used to produce goods and services. The function F( ) embodies the fact that capital and labor can be used in various combinations to produce output.

In the production function above, A is a multiplicative scale factor referred to as total factor productivity (TFP). Note that an increase in TFP implies a proportionate increase in output for any combination of inputs. Hence, TFP reflects the general level of productivity or technology in the economy. The state of technology embodies the cumulative effects of scientific advances, applied research and development, improvements in management methods, and ways of organizing production that raise the productive capacity of factories and offices.

To obtain concrete results, it is useful to use a specific functional form for the production function. The Cobb–Douglas production function, given by:

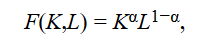
The parameter α determines the shares of output (factor shares) paid by companies to capital and labor and is assumed to have a value between 0 and 1. The reason for this follows from basic microeconomics. In a competitive economy, factors of production are paid their marginal product. Profit maximization requires that the marginal product of capital equal the rental price of capital and the marginal product of labor equal the (real) wage rate. In the case of capital, the marginal product of capital (MPK) for the Cobb–Douglas production function is: (The marginal product of capital is simply the derivative of output with respect to capital. This relationship can be approximated as ΔY/ΔK ≈ [A(K + ΔK)^αL^1−α − AK^αL^1−α]/ΔK ≈ [AαK^α−1ΔKL^1−α]/ΔK = AαK^α−1L^1-α= αY/K. The approximation becomes exact for very small increments, ΔK.)

If we solve this equation for α, we find that it equals the ratio of capital income, rK, to output or GDP, Y. Thus, α is the share of GDP paid out to the suppliers of capital. A similar calculation shows that 1 − α is the share of income paid to labor. This result is important because it is easy to estimate α for an economy by simply looking at capital’s share of income in the national income accounts.

The Cobb–Douglas production function exhibits two important properties that explain the relationship between the inputs and the output. First, the Cobb–Douglas production function exhibits constant returns to scale. This means that if all the inputs into the production process are increased by the same percentage, then output rises by that percentage. Under the assumption of constant returns to scale, we can modify the production function F(K,L) =K^αL^1−α and examine the determinants of the quantity of output per worker. Multiplying the production function by 1/L gives:

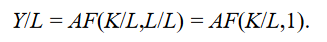
Defining y = Y/L as the output per worker or (average) labor productivity and k = K/L as the capital-to-labor ratio, the expression becomes:

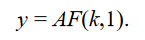
Specifying the Cobb–Douglas production function in output per worker terms, where again lower case letters denote variables measured on a per capita basis, we get

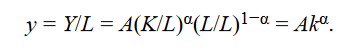
This equation tells us that the amount of goods a worker can produce (labor productivity) depends on the amount of capital available for each worker (capital-to-labor ratio), technology or TFP, and the share of capital in GDP (α). It is important to note that this equation contains two different measures of productivity or efficiency. Labor productivity measures the output produced by a unit of labor, dividing the output (GDP) by the labor input used to produce that output (y = Y/L). TFP is a scale factor that multiplies the impact of the capital and labor inputs.

A second important property of the model is the relation between an individual input and the level of output produced. The Cobb–Douglas production function exhibits diminishing marginal productivity with respect to each individual input. Marginal productivity is the extra output produced from a one-unit increase in an input keeping the other inputs unchanged. It applies to any input as long as the other inputs are held constant. For example, if we have a factory of a fixed size and we add more workers to the factory, the marginal productivity of labor measures how much additional output each additional worker will produce. Diminishing marginal productivity means that at some point, the extra output obtained from each additional unit of the input will decline. To continue our example, if we hire more workers at the existing factory (fixed capital input in this case), each additional worker adds less to output than the previously hired worker does, and average labor productivity (y) falls.

The significance of diminishing marginal returns in the Cobb–Douglas production function depends on the value of α. A value of α close to zero means diminishing marginal returns to capital are very significant and the extra output made possible by additional capital declines quickly as capital increases. In contrast, a value of α close to one means that the next unit of capital increases output almost as much as the previous unit of capital. In this case, diminishing marginal returns still occur but the impact is relatively small. Note that the exponents on the K and L variables in the Cobb–Douglas production function sum to one, indicating constant returns to scale—that is, there are no diminishing marginal returns if both inputs are increased proportionately.

Growth Accounting

Since the publication of Solow’s seminal work (Solow 1957), growth accounting has been used to analyze the performance of economies. The growth accounting equation is essentially the production function written in the form of growth rates. It starts with the Cobb–Douglas production function and decomposes the percentage change in output into components attributable to capital, labor, and technology:

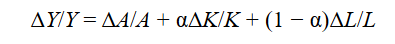
The growth accounting equation states that output growth equals the sum of the rate of technological change, α times the growth rate of capital, and (1 − α) times the growth rate of labor. Here, α represents the elasticity of output with respect to capital, while (1 − α) represents the elasticity with respect to labor. In the Cobb-Douglas production function, these exponents also represent the income shares for capital and labor. Unspecified inputs, such as natural resources, are included in the total factor productivity (TFP) term.

In developed countries, data on output, capital, labor, and the elasticities of these factors are widely available. Technological change, or TFP, must be estimated since it is not directly observable. The elasticities of capital and labor, which are the income shares of these factors, can be derived from national GDP accounts. For instance, in the U.S., labor’s share is about 0.7, and capital’s share is 0.3. This implies that a 1% increase in labor contributes more to GDP growth than a similar increase in capital. For example, with capital’s share at 0.3, a 1% rise in capital raises output by only 0.3%, while an equivalent rise in labor boosts output by 0.7%.

The growth accounting equation serves several purposes. First, Solow used it to estimate the role of technological progress in economic growth by solving for TFP as the residual. This residual captures output growth unexplained by capital and labor inputs and represents technological advancement.

Second, the equation helps quantify the contributions of different factors to long-term economic growth, answering questions about the importance of labor, capital deepening, and TFP. It can be extended to account for variations in labor and capital, such as human and knowledge capital, and can assess the quality of these inputs.

Lastly, the equation is used to estimate potential output. Potential GDP is calculated using trend data for labor, capital, and an estimate of α. Estimating TFP growth is challenging, as it is treated as exogenous and calculated as the residual growth after accounting for inputs. Expanding the production function to include additional inputs requires adjusting the residual calculation to account for their weighted growth rates. Standard methods estimate TFP using time-series models.

An alternative approach is the labor productivity growth accounting equation, which simplifies the process by modeling potential GDP as a function of labor input and labor productivity. This method avoids the need to estimate capital inputs and TFP separately, but it can obscure the distinctions between capital deepening and TFP, making long-term predictions harder. Under this method, potential GDP is estimated using labor productivity growth.

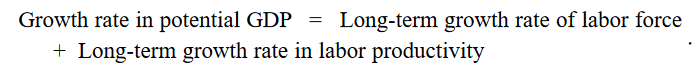
Thus, potential GDP growth is a combination of the long-term growth rate of the labor force and the long-term growth rate of labor productivity. If the labor force is growing at 1% per year and productivity per worker is rising at 2% per year, then potential GDP is rising at 3% per year.

Extending the Production Function

As a simplification, the production function in Equation 1 focused on only the labor and capital inputs. A more complete specification of the production function expands the list of inputs to include the following:

Raw materials: natural resources such as oil, lumber, and available land (N)
Quantity of labor: the number of workers in the country (L)
Human capital: education and skill level of these workers (H)
Information, computer, and telecommunications (ICT) capital: computer hardware, software, and communication equipment (KIT)
Non-ICT capital: transport equipment, metal products and plant machinery other than computer hardware and communications equipment, and non-residential buildings and other structures (KNT)
Public capital: infrastructure owned and provided by the government (KP)
Technological knowledge: the production methods used to con

The expanded production function is expressed mathematically as

Y = AF(N,L,H,K_IT,K_NT,K_P).

The impact of each of these inputs on economic growth is addressed in the following sections.

Capital Deepening vs. Technological Progress

The property of diminishing marginal returns plays an important role in assessing the contribution of capital and technology to economic growth. Exhibit 3 shows the relationship between per capita output and the capital-to-labor ratio. It shows that adding more and more capital to a fixed number of workers increases per capita output but at a decreasing rate. Looking at Exhibit 3 and Example 3, we can think of growth in per capita output coming from two sources: capital deepening and an improvement in technology, often referred to as technological progress.

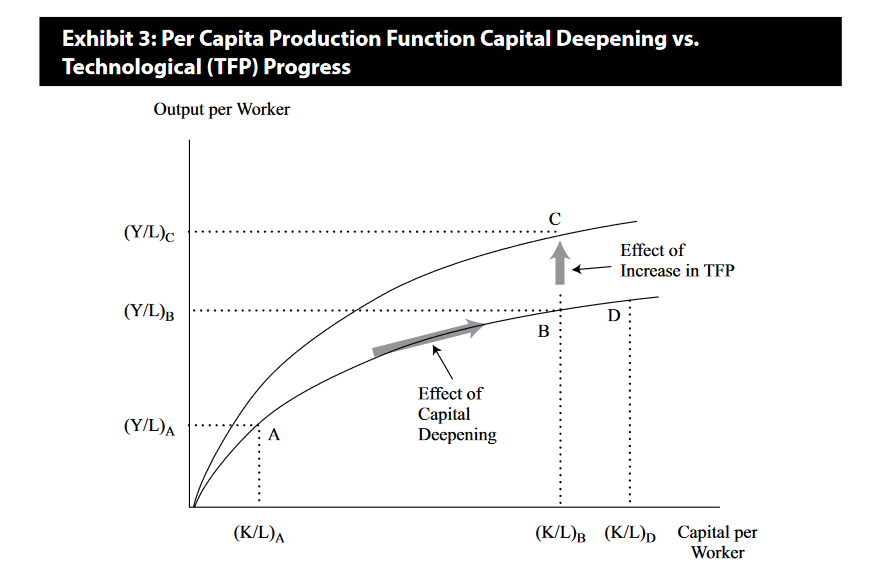
In summary, sustained growth in per capita output requires progress in TFP (technological progress). The neoclassical model’s stark implication that more-rapid capital accumulation —that is, higher rates of investment—cannot result in a permanently higher rate of per capita growth. At the point at which the marginal product of capital equals its marginal cost, profit maximizing producers will stop adding capital

Natural resources

There are two categories of natural resources:

Renewable resources are those that can be replenished, such as a forest. For example, if a tree is cut, a seedling can be planted and a new forest harvested in the future.
Non-renewable resources are finite resources that are depleted once they are consumed. Oil and coal are examples.

Even though access to natural resources (e.g., via trade) is important, ownership and production of natural resources is not necessary for a country to achieve a high level of income. For some countries, the presence of natural resources may even restrain growth, resulting in a “resource curse.” There are two main reasons why this may occur.

First, countries rich in natural resources may fail to develop the economic institutions necessary for growth.
Second, countries rich in resources may suffer the Dutch disease, where currency appreciation driven by strong export demand for resources makes other segments of the economy, in particular manufacturing, globally uncompetitive.

Labor supply

2.6 Explain how demographics, immigration, and labor force participation affect the rate and sustainability of economic growth

The labor force is defined as the working age population (ages 16 to 64) that is either employed or available for work but not working (i.e., unemployed). Thus, growth in the labor input depends on four factors: population growth, labor force participation, net migration, and average hours worked.

Population Growth
- Long-term projections of the labor supply are largely determined by the growth of the working age population. Population growth is determined by fertility rates and mortality rates. Population growth rates are significantly lower in the developed countries than in the developing countries. As a result, there is an ongoing decline in the developed countries’ share of the world’s population. Note that although population growth may increase the growth rate of the overall economy, it has no impact on the rate of increase in per capita GDP.
- The age mix of the population is also important. The percentage of the population over the age of 65 and the percentage below the age of 16 are key considerations. Some of the developed countries, especially European countries, Japan, and South Korea, are facing a growing demographic burden as the portion of non-working elders (over 65) grows as a share of the population. In contrast, growth in many developing countries will receive a demographic boost as the fraction of the population below the age of 16 begins to decline. Interestingly, China is similar to the advanced economies, with a growing proportion of the population over age 65.
Labor Force Participation
- In the short run, the labor force growth rate may differ from population growth because of changes in the participation rate. The labor force participation rate is defined as the percentage of the working age population in the labor force. It has trended upward in most countries over the last few decades because of rising participation rates among women. In contrast to population, an increase in the participation rate may raise the growth of per capita GDP. In many southern European countries, such as Greece and Italy, the participation rate among women is well below the rates in the United States and northern European countries (see Exhibit 5). Thus, rising participation rates among women in these countries could increase growth in the labor force and in potential GDP. This has been the case for Spain, where the female labor force participation rate rose from 52.0% in 2000 to 67.9% in 2018. It should be noted, however, that rising or falling labor force participation is likely to represent a transition to a new higher or lower level of participation rather than a truly permanent rate of change. Thus, although trends in participation may contribute to or detract from potential growth for substantial periods, one should be cautious in extrapolating such trends indefinitely.
Net Migration
- Another factor increasing economic and population growth, especially among the developed countries, is immigration. Heightened immigration is a possible solution to the slowing labor force growth being experienced by many developed countries with low birthrates within the native population. The growth rate of the labor force in Ireland, Spain, the United Kingdom, and the United States has increased between 2000 and 2010 because of immigration, although it slowed substantially in the 2010–2018 period. Focusing on the decade starting in 2000, Exhibit 4 shows the population growth rates for Ireland and Spain at 1.71% and 1.35%, respectively. The population growth rates were well above the population growth rates in other European countries. As shown in Exhibit 6, this is because of the impact of immigration. The open-border policies of both countries led to a significant population of immigrants that contributed to a large increase in labor input for both countries. As a consequence, both countries experienced GDP growth above the European average during this period (see Exhibit 1).
Average Hours Worked
- The contribution of labor to overall output is also affected by changes in the average hours worked per worker. Average hours worked is highly sensitive to the business cycle. The long-term trend in average hours worked, however, has been toward a shorter work week in the advanced countries. This development is the result of legislation, collective bargaining agreements, the growth of part-time and temporary work, and the impact of both the “wealth effect” and high tax rates on labor income, which cause workers in high-income countries to value leisure time relatively more highly than labor income.
- Exhibit 7 provides data on average hours worked per year per person in the labor force for selected years since 1995. For most countries, the average number of hours worked per year has been declining. There is also a significant difference in hours worked across countries. In 2018, average hours worked per year in South Korea, at 1,993 hours, were 46.1% more than the 1,363 average hours worked per year in Germany. The increase in female labor force participation rates may be contributing to the shorter average workweek because female workers disproportionately take on part-time, rather than full-time, jobs.
Labor Quality: Human Capital
- In addition to the quantity of labor, the quality of the labor force is an important source of growth for an economy. Human capital is the accumulated knowledge and skills that workers acquire from education, training, or life experience. In general, better-educated and more-skilled workers will be more productive and more adaptable to changes in technology or other shifts in market demand and supply.
- An economy’s human capital is increased through investment in education and on-the-job training. Like physical capital, investment in education is costly, but studies show that there is a significant return on that investment. That is, people with more education earn higher wages. In addition, education may also have a spillover or externality impact. Increasing the educational level of one person raises not only the output of that person but also the output of those around that person. The spillover effect operates through the link between education and advances in technology. Education not only improves the quality of the labor force, and thus the stock of human capital, but also encourages growth through innovation. Importantly, increased education, obtained both formally and via on-the-job training, could result in a permanent increase in the growth rate of an economy if the more educated workforce results in more innovations and a faster rate of technological progress. Investment in the population’s health is also a major contributor to human capital, especially in developing countries.

ICT, Non-ICT, and technology and public infrastructure

2.7 Explain how investment in physical capital, human capital, and technological development affects economic growth

ICT and Non ICT

These studies suggest that capital spending could be separated into two categories.
ICT: Spending on information, computers, and telecommunications equipment (ICT investment), The IT sector has grown very rapidly and has made a significant contribution to increasing the rate of economic and productivity growth. The greater use of IT equipment in various industries has resulted in network externalities. Computers allow people to interconnect through the internet and by email, enabling them to work more productively. The more people in the network, the greater the potential productivity gains.
Non ICT: Non-ICT capital spending includes non-residential construction, transport equipment, and machinery.
High levels of capital spending for Non ICT should eventually result in capital deepening and thus have less impact on potential GDP growth.
In contrast, a growing share of ICT investments in the economy, through their externality impacts, may actually boost the growth rate of potential GDP.

Technology

The most important factor affecting growth of per capita GDP is technology, especially in developed countries.
Technological change can be embodied in human capital (knowledge, organization, information, and experience base) and/or in new machinery, equipment, and software. Therefore, high rates of investment are important, especially investment in ICT goods.
Countries can also innovate through expenditures, both public and private, on research and development (R&D). Expenditures on R&D and the number of patents issued, although not directly measuring innovation, provide some useful insight into innovative performance.

Public Infrastructure

The final expansion of the definition of the capital input is public infrastructure investment.
Roads, bridges, municipal water, dams and, in some countries, electric grids are all examples of public capital.
They have few substitutes and are largely complements to the production of private sector goods and services.
Infrastructure investment is an important source of productivity growth and should be included as an input in the production function.

Summary of economic growth determinants

The factors of production include

human capital
ICT and non-ICT capital (the supply of non-ICT and ICT capital)
public capital (also known as public Infrastructure)
labor (the quantity and quality of labor)
natural resources (aw materials)
technological knowledge

Theories of growth

2.8 Compare classical growth theory, neoclassical growth theory, and endogenous growth theory

Classical growth theory was developed by Thomas Malthus in his 1798 publication Essay on the Principle of Population.

The classical model predicts that in the long run, the adoption of new technology results in a larger but not richer population. Thus, the standard of living is constant over time even with technological progress, and there is no growth in per capita output
The prediction from the Malthusian model failed for two reasons:
- 1. The link between per capita income and population broke down. In fact, as the growth of per capita income increased, population growth slowed rather than accelerating as predicted by the classical growth model.
- 2. Growth in per capita income has been possible because technological progress has been rapid enough to more than offset the impact of diminishing marginal returns.
Because the classical model’s pessimistic prediction never materialized, economists changed the focus of the analysis away from labor to capital and to the neoclassical model.

Robert Solow devised the mainstream neoclassical theory of growth in the 1950s (Solow 1957). The heart of this theory is the Cobb–Douglas production function discussed earlier. As before, the potential output of the economy is given by

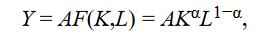
where K is the stock of capital, L is the labor input, and A is total factor productivity. In the neoclassical model, both capital and labor are variable inputs each subject to diminishing marginal productivity.

The objective of the neoclassical growth model is to determine the long-run growth rate of output per capita and relate it to (a) the savings/investment rate, (b) the rate of technological change, and (c) population growth.

Balanced or Steady-State Rate of Growth

As with most economic models, the neoclassical growth model attempts to find the equilibrium position toward which the economy will move. In the case of the Solow model, this equilibrium is the balanced or steady-state rate of growth that occurs when the output-to-capital ratio is constant. Growth is balanced in the sense that capital per worker and output per worker grow at the same rate. We begin the analysis by using the per capita version of the Cobb–Douglas production function given earlier:

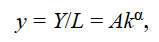
where k = K/L (that is capital-to-labor ratio (k)). Using their definitions, the rates of change of capital per worker and output per worker are given by

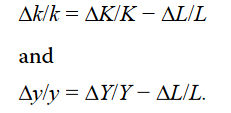
Derivation: We take log transfer for k = K/L, and take the derivation of time for both side

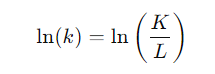
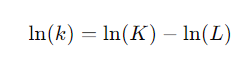
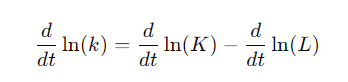
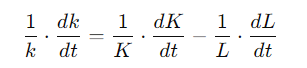
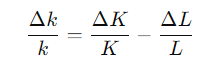
From the production function, the growth rate of output per worker is also equal to

The physical capital stock in an economy will increase because of gross investment (I) and decline because of depreciation. In a closed economy, investment must be funded by domestic saving. Letting s be the fraction of income (Y) that is saved, gross investment is given by I = sY. Assuming the physical capital stock depreciates at a constant rate, δ, the change in the physical capital stock is given by

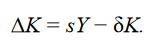
Subtracting labor supply growth, ΔL/L ≡ n, and rearranging gives

In the steady state, the growth rate of capital per worker is equal to the growth rate of output per worker. Thus, (From eqution (6))

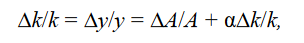
from which we get

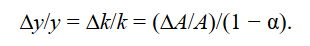
Letting θ denote the growth rate of TFP (i.e., ∆A/A), we see that the equilibrium sustainable growth rate of output per capita (∆y/y) is a constant that depends only on the growth rate of TFP (θ) and the elasticity of output with respect to capital (α). Adding back the growth rate of labor (n) gives the sustainable growth rate of output.

Growth rate of output per capita = ∆y/y

Growth rate of output = ∆Y/Y

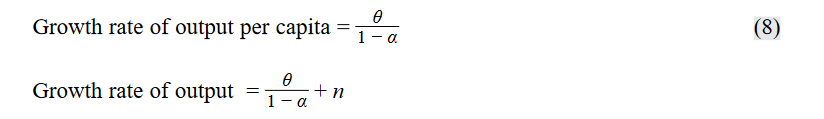
recall that y = Y/L

∆y/y = ∆Y/Y – ∆L/L, so ∆Y/Y (Growth rate of output) = ∆y/y (Growth rate of output per capita) + ∆L/L (growth rate of labor)

This is the key result of the neoclassical model. Note that θ/(1 − α) is the steady-state growth rate of labor productivity, so Equation 8 is consistent with the labor productivity growth accounting equation discussed earlier. Substituting θ/(1 − α) into the left-hand side of Equation 7 and rearranging gives the equilibrium output-to-capital ratio, denoted by the constant Ψ.

In the steady state, the output-to-capital ratio is constant and the capital-to-labor ratio (k) and output per worker (y) grow at the same rate, given by θ/(1 − α). On the steady-state growth path, the marginal product of capital is also constant and, given the Cobb–Douglas production function, is equal to α(Y/K). The marginal product of capital is also equal to the real interest rate in the economy. Note that even though the capital-to-labor ratio (k) is rising at rate θ/(1 − α) in the steady state, the increase in the capital-to-labor ratio (k) has no impact on the marginal product of capital, which is not changing. Capital deepening is occurring, but it has no effect on the growth rate of the economy or on the marginal product of capital once the steady state is reached.

An intuitive way to understand the steady-state equilibrium given in Equation 9 is to transform it into a savings/investment equation:

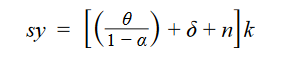
Steady-state equilibrium occurs at the output-to-capital ratio where the savings and actual gross investment per worker generated in the economy (sy) are just sufficient to (1) provide capital for new workers entering the workforce at rate n, (2) replace plant and equipment wearing out at rate δ, and (3) deepen the physical capital stock at the rate θ/(1 − α) required to keep the marginal product of capital equal to the rental price of capital. Exhibit 12 shows the steady-state equilibrium graphically. The straight line in the exhibit indicates the amount of investment required to keep the physical capital stock growing at the required rate. Because the horizontal axis is capital per worker, the slope of the line is given by [δ + n + θ/(1 − α)]. The curved line shows the amount of actual investment per worker and is determined by the product of the saving rate and the production function. It is curved because of diminishing marginal returns to the capital input in the production function. The intersection of the required investment and actual investment lines determines the steady state. Note that this exhibit is a snapshot at a point in time. Over time, the capital-to-labor ratio rises at rate [θ/ (1 − α)] as the actual saving/investment curve [sf(k)] shifts upward because of TFP growth, and the equilibrium moves upward and to the right along the straight line.

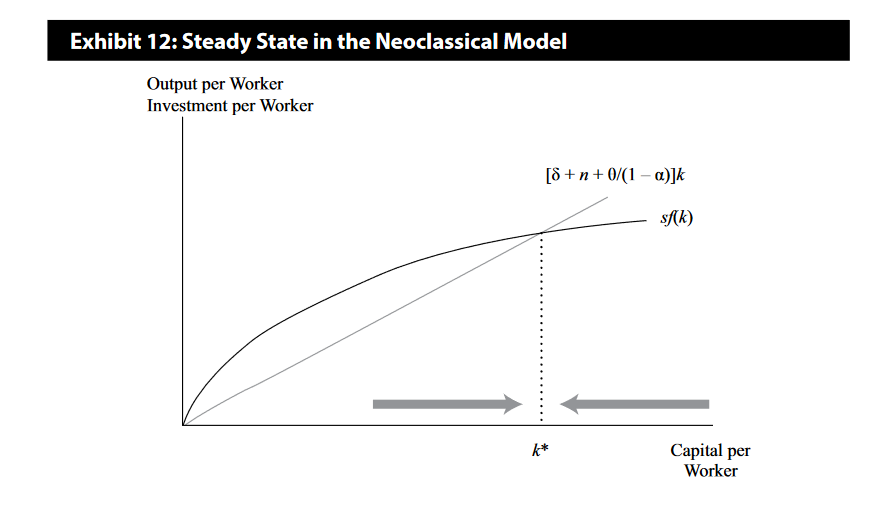
The impact of the various parameters in the model on the steady state can also be seen in the exhibit. At any point in time when the economy is on its steady-state growth path, the exogenous factors—labor supply and TFP—are fixed. We would like to know what effect each of the parameters in the model has on the steady-state capital-to-labor ratio and therefore on output per worker. For example, if there are two economies that differ only with respect to one parameter, what does that imply about their per capita incomes? All else the same, we can say the following regarding the impact of the parameters:

Saving rate (s): An increase in the saving rate implies a higher capital-to-labor ratio (k) and higher output per worker (y) because a higher saving rate generates more saving/investment at every level of output. In Exhibit 13, the saving/investment curve [sf(k)] shifts upward from an initial steady-state equilibrium at point A to a new equilibrium at point B. At the new equilibrium point, it intersects the required investment line [δ + n + θ/(1 − α)] at higher capital-to-labor and output per worker ratios. Note that although the higher saving rate increases both k and y, it has no impact on the steadystate growth rates of output per capita or output (Equation 8).
Labor force growth (n): An increase in the labor force growth rate reduces the equilibrium capital-to-labor ratio because a corresponding increase in the steady-state growth rate of capital is required. Given the gross saving/investment rate, this can be achieved only at a lower capital-to-labor ratio. Output per worker is correspondingly lower as well. In Exhibit 14, the higher population growth rate increases the slope of the required investment line. This shifts the steady-state equilibrium from point A to point B, where it intersects the supply of saving/investment curve at lower capital-to-labor and output per worker ratios.
Depreciation rate (δ): An increase in the depreciation rate reduces the equilibrium capital-to-labor and output per worker ratios because a given rate of gross saving generates less net capital accumulation. Graphically, it increases the slope of the required investment line and affects the steady-state equilibrium in the same way as labor force growth (Exhibit 14).
Growth in TFP (θ): An increase in the growth rate of TFP reduces the steady-state capital-to-labor ratio and output per worker for given levels of labor input and TFP. This result must be interpreted with care. Raising the growth rate of TFP means that output per worker will grow faster in the future (Equation 8), but at a given point in time, a given supply of labor, and a given level of TFP, output per worker is lower than it would be with a slower TFP growth rate. In effect, the economy is on a steeper trajectory off a lower base of output per worker. Graphically, it is identical to Exhibit 14 in that faster TFP growth steepens the required investment line (increases the slope), which intersects with the available saving/investment curve at lower capital-to-labor and investment per worker ratios.
The slope is [δ + n + θ/(1 − α)]

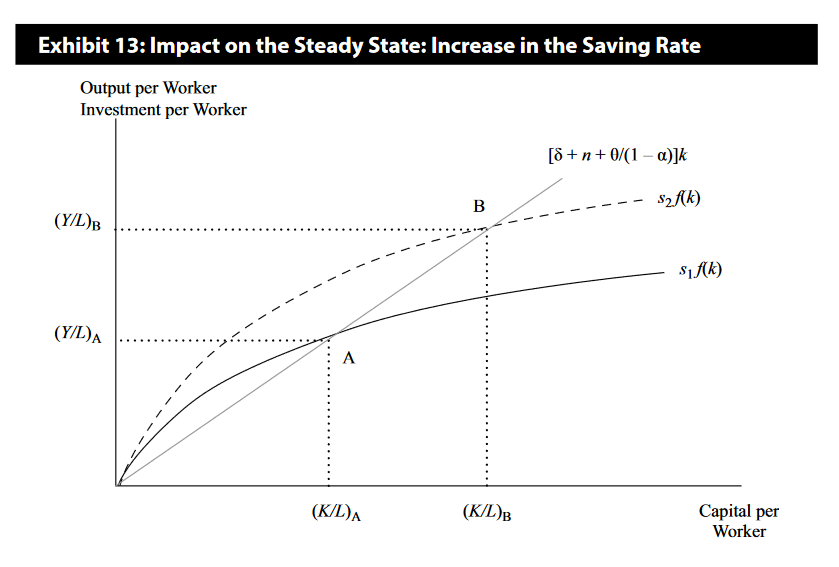
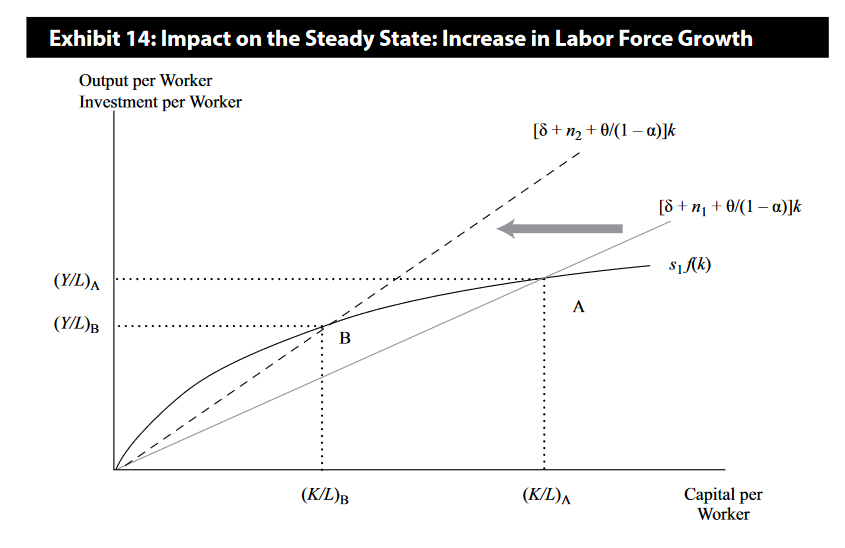
In sum, such factors as the saving rate, the growth rate of the labor force, and the depreciation rate change the level of output per worker but do not permanently change the growth rate of output per worker. A permanent increase in the growth rate in output per worker can occur only if there is a change in the growth rate of TFP. So far we have focused on the steady-state growth path. What happens if the economy has not yet reached the steady state? During the transition to the steady-state growth path, the economy can experience either faster or slower growth relative to the steady state. Using Equations 6, 7, and 9, we can write the growth rates of output per capita and the capital-to-labor ratio as, respectively,

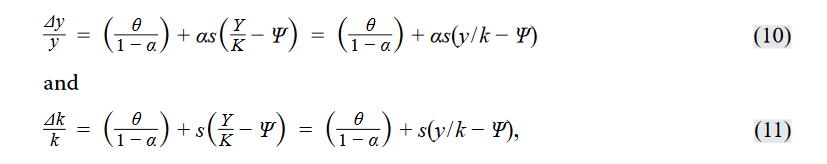
where the second equality in each line follows from the definitions of y and k, which imply (Y/K) = y/k. These relationships are shown in Exhibit 15.

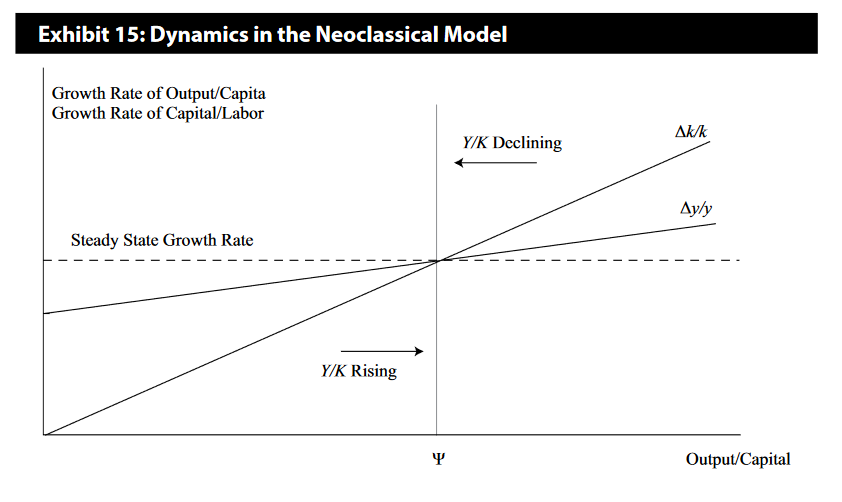
If the output-to-capital ratio is above its equilibrium level (ψ), the second term in Equations 10 and 11 is positive and the growth rates of output per capita and the capital-to-labor ratio are above the steady-state rate θ/(1 − α). This corresponds to a situation in which actual saving/investment exceeds required investment and above-trend growth in per capita output is driven by an above-trend rate of capital deepening. This situation usually reflects a relatively low capital-to-labor ratio but could, at least in principle, arise from high TFP. Because α < 1, capital is growing faster than output and the output-to-capital ratio is falling. Over time, the growth rates of both output per capita and the capital-to-labor ratio decline to the steady-state rate.

Of course, the converse is true if the output-to-capital ratio is below its steady-state level. Actual investment is insufficient to sustain the trend rate of growth in the capital-to-labor ratio, and both output per capita and the capital-to-labor ratio grow more slowly. This situation usually corresponds to a relatively high and unsustainable capital-to-labor ratio, but it could reflect relatively low TFP and hence relatively low output. Over time, output grows faster than capital, the output-to-capital ratio rises, and growth converges to the trend rate.

Implications of neoclassical model

There are four major groups of conclusions from the neoclassical model:

1. Capital Accumulation
- a. Capital accumulation affects the level of output but not the growth rate in the long run.
- b. Regardless of its initial capital-to-labor ratio or initial level of productivity, a growing economy will move to a point of steady-state growth.
- c. In a steady state, the growth rate of output equals the rate of labor force growth plus the rate of growth in TFP scaled by labor’s share of income [n + θ/(1 − α)]. The growth rate of output does not depend on the accumulation of capital or the rate of business investment. Those familiar with the “labor-augmenting” technical change formulation of the neoclassical model should note that in that formulation, the rate of labor-augmenting technical change is also the growth rate of labor productivity. In our formulation, the growth rate of labor productivity is θ/(1 − α). So both formulations imply that long-run growth equals the growth rate of the labor supply (n) plus a constant growth rate of labor productivity.
Capital Deepening vs. Technology
- a. Rapid growth that is above the steady-state rate of growth occurs when countries first begin to accumulate capital; but growth will slow as the process of accumulation continues (see Exhibit 16).
- b. Long-term sustainable growth cannot rely solely on capital deepening investment—that is, on increasing the stock of capital relative to labor. If the capital-to-labor ratio grows too rapidly (i.e., faster than labor productivity), capital becomes less productive, resulting in slower rather than faster growth.
- c. More generally, increasing the supply of some input(s) too rapidly relative to other inputs will lead to diminishing marginal returns and cannot be the basis for sustainable growth.
- d. In the absence of improvements in TFP, the growth of labor productivity and per capita output would eventually slow.
- e. Because of diminishing marginal returns to capital, the only way to sustain growth in potential GDP per capita is through technological change or growth in total factor productivity. This results in an upward shift in the production function—the economy produces more goods and services for any given mix of labor and capital inputs.
3. Convergence
- a. Given the relative scarcity and hence high marginal productivity of capital and potentially higher saving rates in developing countries, the growth rates of developing countries should exceed those of developed countries.
- b. As a result, there should be a convergence of per capita incomes between developed and developing countries over time.
4. Effect of Savings on Growth
- a. The initial impact of a higher saving rate is to temporarily raise the rate of growth in the economy. Mathematically, this can be seen as follows: Equation 9 indicates that an increase in the saving rate (s) reduces the steady-state output-to-capital ratio (ψ). This makes the last term in Equations 10 and 11 positive, raising the growth rates of output per capita (y) and the capital-to-labor ratio (k) above the steady-state rate. In response to the higher saving rate, growth exceeds the steady-state growth rate during a transition period. However, the economy returns to the balanced growth path after the transition period.
- b. During the transition period, the economy moves to a higher level of per capita output and productivity.
- c. Once an economy achieves steady-state growth, the growth rate does not depend on the percentage of income saved or invested. Higher savings cannot permanently raise the growth rate of output. d. Countries with higher saving rates, however, will have a higher level of per capita output, a higher capital-to-labor ratio, and a higher level of labor productivity.

Extension of neoclassical model

Solow (1957) used the growth accounting equation to determine the contributions of each factor to economic growth in the United States for the period 1909–1949. He reached the surprising conclusion that more than 80% of the per capita growth in the United States resulted from TFP. Denison (1985) authored another study examining US growth for the period 1929–1982 using the Solow framework. His findings were similar to Solow’s, with TFP explaining nearly 70% of US growth. The problem with these findings is that the neoclassical model provides no explicit explanation of the economic determinants of technological progress or how TFP changes over time. Because technology is determined outside the model (i.e., exogenously), critics argue that the neoclassical model ignores the very factor driving growth in the economy. Technology is simply the residual or the part of growth that cannot be explained by other inputs, such as capital and labor. This lack of an explanation for technology led to growing dissatisfaction with the neoclassical model.

The other source of criticism of the neoclassical model is the prediction that the steady-state rate of economic growth is unrelated to the rate of saving and investment. Long-run growth of output in the Solow model depends only on the rates of growth of the labor force and technology. Higher rates of investment and savings have only a transitory impact on growth. Thus, an increase in investment as a share of GDP from 10% to 15% of GDP will have a positive impact on the near-term growth rate but will not have a permanent impact on the ultimately sustainable percentage growth rate. This conclusion makes many economists uncomfortable. Mankiw (1995) provided evidence rebutting this hypothesis and showed that saving rates and growth rates are positively correlated across countries. Finally, the neoclassical model predicts that in an economy where the stock of capital is rising faster than labor productivity, the return to investment should decline with time. For the advanced countries, the evidence does not support this argument because returns have not fallen over time.

Critiques of the neoclassical model led to two lines of subsequent research on economic growth. The first approach, originated by Jorgenson (1966, 2000), is termed the augmented Solow approach. It remains in the neoclassical tradition in that diminishing marginal returns are critical and there is no explanation for the determinants of technological progress. Instead, this approach attempts to reduce empirically the portion of growth attributed to the unexplained residual labeled technological progress (TFP). The idea is to develop better measures of the inputs used in the production function and broaden the definition of investment by including human capital, research and development, and public infrastructure. In addition, the composition of capital spending is important. Higher levels of capital spending on high-technology goods will boost productivity more than spending on machine tools or structures.

By adding inputs such as human capital to the production function, the augmented Solow model enables us to more accurately measure the contribution of technological progress to growth. The economy still moves toward a steady-state growth path, however, because even broadly defined capital is assumed to eventually encounter diminishing marginal returns. In essence, this line of research uses the growth accounting methodology and increases the number of inputs in the production function in order to provide a more accurate measure of technological progress. The second approach is the endogenous growth theory, which we examine in the next section.

Endogenous growth theory

The alternative to the neoclassical model is a series of models known as endogenous growth theory. These models focus on explaining technological progress rather than treating it as exogenous. In these models, self-sustaining growth emerges as a natural consequence of the model and the economy does not necessarily converge to a steady-state rate of growth. Unlike the neoclassical model, there are no diminishing marginal returns to capital for the economy as a whole in the endogenous growth models. So increasing the saving rate permanently increases the rate of economic growth. These models also allow for the possibility of increasing returns to scale.

Romer (1986) provided a model of technological progress and a rationale for why capital does not experience diminishing marginal returns. He argued that capital accumulation is the main factor accounting for long-run growth, once the definition of capital is broadened to include such items as human or knowledge capital and research and development (R&D). R&D is defined as investment in new knowledge that improves the production process. In endogenous growth theory, knowledge or human capital and R&D spending are factors of production, like capital and labor, and have to be paid for through savings.

Companies spend on R&D for the same reason they invest in new equipment and build new factories: to make a profit. R&D spending is successful if it leads to the development of a new product or method of production that is successful in the marketplace. There is a fundamental difference, however, between spending on new equipment and factories and spending on R&D. The final product of R&D spending is ideas. These ideas can potentially be copied and used by other companies in the economy. Thus, R&D expenditures have potentially large positive externalities or spillover effects. This means that spending by one company has a positive impact on other companies and increases the overall pool of knowledge available to all companies. Spending by companies on R&D and knowledge capital generates benefits to the economy as a whole that exceed the private benefit to the individual company making the R&D investment. Individual companies cannot fully capture all the benefits associated with creating new ideas and methods of production. Some of the benefits are external to the company, and so are the social returns associated with the investment in R&D and human capital.

This distinction between the private and social returns or benefits to capital is important because it solves an important microeconomic issue. The elimination of the assumption of diminishing marginal returns to capital implies constant returns to capital and increasing returns to all factors taken together. If individual companies could capture these scale economies, then all industries would eventually be dominated by a single company—a monopoly. There is simply no empirical evidence to support this implication. Separating private returns from social returns solves the problem. If companies face constant returns to scale for all private factors, there is no longer an inherent advantage for a company being large. But the externality or social benefit results in increasing returns to scale across the entire economy as companies benefit from the private spending of the other companies.

The role of R&D spending and the positive externalities associated with this spending have important implications for economic growth. In the endogenous growth model, the economy does not reach a steady growth rate equal to the growth of labor plus an exogenous rate of labor productivity growth. Instead, saving and investment decisions can generate self-sustaining growth at a permanently higher rate. This situation is in sharp contrast to the neoclassical model, in which only a transitory increase in growth above the steady state is possible. The reason for this difference is that because of the externalities on R&D, diminishing marginal returns to capital do not set in. The production function in the endogenous growth model is a straight line given by

where output per worker (y_e) is proportional to the stock of capital per worker (k_e), c is the (constant) marginal product of capital in the aggregate economy, and the subscript e denotes the endogenous growth model. In contrast, the neoclassical production function is a curved line that eventually flattens out (see Exhibit 4).

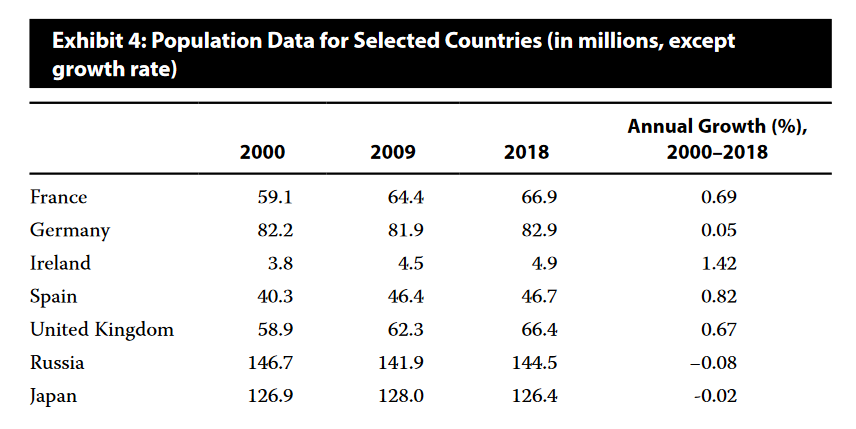
To understand the significance of introducing constant returns to aggregate capital accumulation, note that in this model the output-to-capital ratio is fixed (= c) and therefore output per worker (k_e) always grows at the same rate as capital per worker (k_e). Thus, faster or slower capital accumulation translates one for one into faster or slower growth in output per capita. Substituting Equation 12 into Equation 7 gives an equation for the growth rate of output per capita in the endogenous growth model:

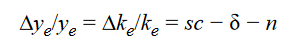
Because all the terms on the right-hand side of this equation are constant, this is both the long-run and the short-run growth rate in this model. Examination of the equation shows that a higher saving rate (s) implies a permanently higher growth rate. This is the key result of the endogenous growth model.

The positive externalities associated with spending on R&D and knowledge capital suggest that spending by private companies on these inputs may be too low from an overall societal point of view. This is an example of a market failure wherein private companies under-invest in the production of these goods. In this case, there may be a role for government intervention to correct for the market failure by direct government spending on R&D and/or providing tax breaks and subsidies for private production of knowledge capital. Higher levels of spending on knowledge capital could translate into faster economic growth even in the long run. Finally, according to the endogenous growth theory, there is no reason why the incomes of developed and developing countries should converge. Because of constant or even increasing returns associated with investment in knowledge capital, the developed countries can continue to grow as fast as, or faster than, the developing countries. As a result, there is no reason to expect convergence of income over time. We now turn to the convergence debate in more detail.

Convergence hypotheses

2.9 Explain and evaluate convergence hypotheses

As is evident in Exhibit 1, a wide gap separates the living standards in developed and developing nations. The question is, will this difference persist forever or will the per capita income levels of the developing countries converge to those of the developed countries? Convergence means that countries with low per capita incomes should grow at a faster rate than countries with high per capita incomes. Thus, over time the per capita income of developing countries should converge toward that of the developed countries. Whether convergence occurs has major implications for the future growth prospects of developed versus developing countries. It also has important investment implications.

There are three types of convergence commonly discussed in the economics literature: absolute, conditional, and club convergence. Absolute convergence means that developing countries, regardless of their particular characteristics, will eventually catch up with the developed countries and match them in per capita output. The neoclassical model assumes that all countries have access to the same technology. As a result, per capita income in all countries should eventually grow at the same rate. Thus, the model implies convergence of per capita growth rates among all countries. It does not, however, imply that the level of per capita income will be the same in all countries regardless of underlying characteristics; that is, it does not imply absolute convergence.

Conditional convergence means that convergence is conditional on the countries having the same saving rate, population growth rate, and production function. If these conditions hold, the neoclassical model implies convergence to the same level of per capita output as well as the same steady-state growth rate. In terms of Exhibit 13, these economies would have the same k* and thus the same steady state. If they start with different capital-to-labor ratios, their growth rates will differ in the transition to the steady state. The economy with a lower capital-to-labor ratio will experience more rapid growth of productivity and per capita income, but the differential will diminish until they finally converge. Countries with different saving rates or population growth rates and thus different steady-state values for k* will have different steady-state levels of per capita income, but their growth rates of per capita output will still converge.

The data (see Exhibit 17) indicate that some of the poorer countries are diverging rather than converging to the income levels of the developed countries. Thus, we have the notion of club convergence, where only rich and middle-income countries that are members of the club are converging to the income level of the world’s richest countries. This means that the countries with the lowest per capita income in the club grow at the fastest rate. In contrast, countries outside the club continue to fall behind. Poor countries can join the club if they make appropriate institutional changes, such as those summarized earlier in our discussion of factors limiting growth in developing economies. Finally, countries may fall into a non-convergence trap if they do not implement necessary institutional reforms. For example, failure to reform labor markets has undermined growth in some European countries that have experienced weak growth in employment and high rates of unemployment over the last two decades. Certain institutional arrangements that initially enhance growth may later generate non-convergence traps if maintained too long. Import substitution policies enabled the Latin American countries to grow rapidly in the 1950s and 1960s but caused them to stagnate in the 1970s and 1980s.

If convergence, and especially club convergence, does occur, investing in countries with lower per capita incomes that are members of the club should, over long periods, provide a higher rate of return than investing in higher-income countries. Convergence means that the rate of growth of potential GDP should be higher in developing countries that have made the institutional changes that are a precondition for growth and that enable these countries to become members of the convergence club. With higher long-term growth in these economies, corporate profits should also grow at a faster rate. Given the faster rate of growth in earnings, stock prices may also rise at a faster rate. Of course, risk is also likely to be higher in these markets. Nonetheless, it is reasonable to conclude that long-term investors should allocate a risk-tolerance-appropriate portion of their assets to those developing economies that have become members of the convergence club.

Convergence between the developed and developing countries can occur in two ways. First, convergence takes place through capital accumulation and capital deepening. Exhibit 16 illustrates the difference between developed and developing countries using the per capita neoclassical production function. The developed countries operate at point B, so increases in capital have almost no impact on productivity. In contrast, developing countries operate at point A, where increases in capital significantly boost labor productivity.

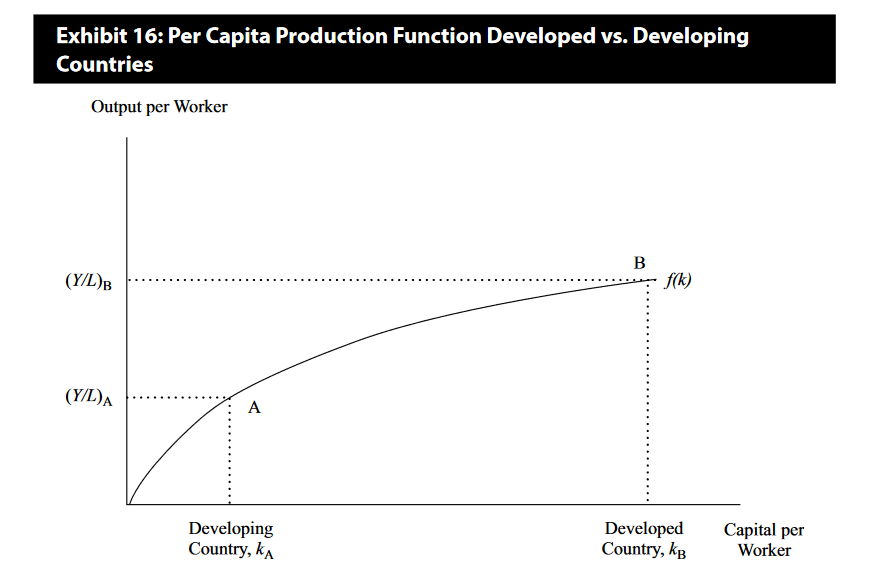
A second source of convergence is that developing countries can imitate or adopt technology already widely utilized in the advanced countries. Developing countries can learn from advanced countries as scientific and management practices spread with globalization. By importing technology from the advanced countries, the developing countries can achieve faster economic growth and converge to the income of the advanced countries. Technology transfers will narrow the income gap between developed and developing countries only if the poor countries invest the resources to master the technology and apply it to their economies. This spending is similar to R&D spending and allows the country to join the convergence club. The steady-state rate of growth for members of the convergence club will be determined by the global rate of technological progress. Without such spending, the country will be left out and will continue to fall behind the developed countries.

In contrast to the neoclassical model, the endogenous growth model makes no prediction that convergence should occur. This model allows for countries that start with high per capita income and more capital to grow faster and stay ahead of the developing countries. If the externalities associated with knowledge and human capital are large, the higher-income country can maintain its lead through high rates of investment in these capital inputs.

If the convergence hypothesis is correct, there should be an inverse relation between the initial level of per capita real GDP and the growth rate in per capita GDP. Exhibit 17 shows the countries in Exhibit 1 in descending order of per capita income in 1950. If incomes are converging across countries, the poor countries in 1950 should have a higher growth rate between 1950 and 2018 than the rich countries.

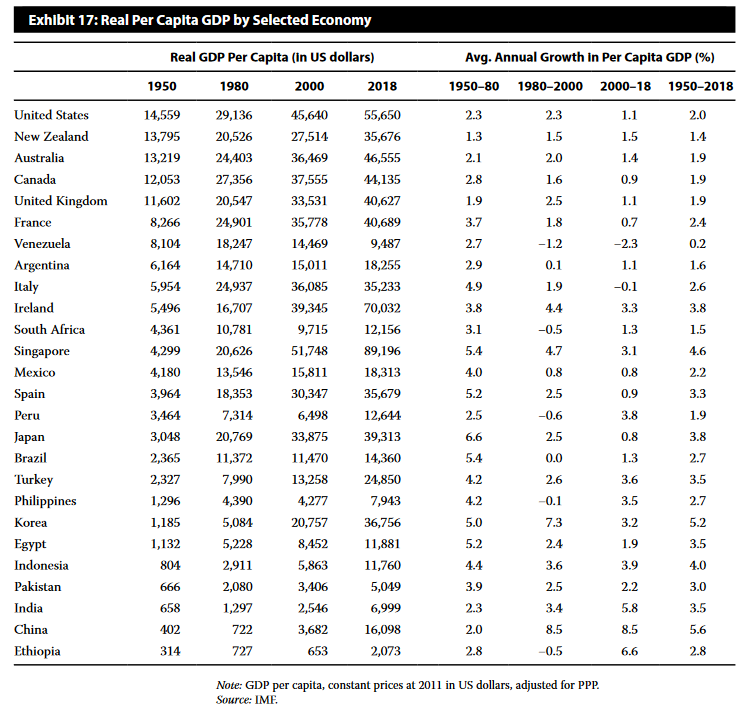
The results for the convergence hypothesis are mixed. The economies with the highest per capita income in 1950 were the United States, New Zealand, Australia, and Canada. The markets with the fastest growth rate over the period 1950–2018 were China and Korea, each growing at a rate above 5%. This result strongly supports convergence because the per capita incomes of these economies in 1950 were well below that of the United States. In addition, the results for Japan, Singapore, Spain, and Korea showed a convergence to the level of income in the advanced economies. In total, 17 of the 27 economies in our sample grew faster than the United States during the period.

However, South Africa, Argentina, Venezuela, and New Zealand were among those that fell further behind the United States. Interestingly, since 2000, convergence has been relatively strong overall, with 16 countries in our sample (60%) growing faster than the United States—including Ethiopia, the Philippines, Peru, Turkey, South Africa, Australia, and New Zealand—but has not continued among the most advanced economies: France, Japan, and Italy all lagged the United States, Canada, and Australia.

The evidence seems to suggest that poorer countries may converge if they develop the appropriate legal, political, and economic institutions. In addition, trade policy is an important factor, which we address in the next section.

Growth in an open economy

2.10 Describe the economic rationale for governments to provide incentives to private investment in technology and knowledge

2.11 Describe the expected impact of removing trade barriers on capital investment and profits, employment and wages, and growth in the economies involved

The Solow model discussed earlier assumed a closed economy in which domestic investment equals domestic savings and there is no international trade or capital flows. Opening up the economy to trade and financial flows can significantly affect the rate of growth in an economy for the following reasons:

1. A country can borrow or lend funds in global markets, and domestic investment can be funded by global savings. Thus, investment is not constrained by domestic savings.
2. Countries can shift resources into industries in which they have a comparative advantage and away from industries in which they are relatively inefficient, thereby increasing overall productivity.
3. Companies have access to a larger, global market for their products, allowing them to better exploit any economies of scale and increasing the potential reward for successful innovation.
4. Countries can import technology, thus increasing the rate of technological progress. 5. Global trade increases competition in the domestic market, forcing companies to produce better products, improve productivity, and keep costs low.

According to the neoclassical model, convergence should occur more quickly if economies are open and there is free trade and international borrowing and lending. Opening up the economy should increase the rate at which countries’ capital-to-labor ratios converge. The dynamic adjustment process can be described as follows:

1. Developing countries have less capital per worker, and as a result, the marginal product of capital is higher. Thus, the rate of return on investments should be higher in countries with low capital-to-labor ratios and lower in countries with high capital-to-labor ratios.
2. Global savers, seeking higher returns on investments, will invest in the capital-poor countries. In an open economy, capital should flow from countries with high capital-to-labor ratios to those that are capital poor.
3. Because of the capital inflows, the physical capital stock in the developing countries should grow more rapidly than in rich countries even if the saving rate is low in the poorer countries. Faster capital growth will result in higher productivity growth, causing per capita incomes to converge.
4. Because capital flows must be matched by offsetting trade flows, capital-poor countries will tend to run a trade deficit as they borrow globally to finance domestic investment. In contrast, the developed countries will tend to run trade surpluses as they export capital.
5. During the transition to the new steady state, the inflows of capital will temporarily raise the rate of growth in the capital-poor country above the steady-state rate of growth. At the same time, growth in the capital-exporting countries will be below the steady state. 6. Over time, the physical capital stock will rise in the capital-poor country, reducing the return on investments. As a result, the rate of investment and size of the country’s trade deficit will decline. Growth will slow and approach the steady-state rate of growth. If investment falls below the level of domestic savings, the country will eventually shift from a trade deficit to a trade surplus and become an exporter of capital. 7. In the Solow model, after the reallocation of world savings, there is no permanent increase in the rate of growth in an economy. Both the developed and developing countries grow at the steady-state rate of growth.

In contrast to the neoclassical model, endogenous growth models predict that a more open trade policy will permanently raise the rate of economic growth. In these models, international trade increases global output through the following:

1. A selection effect, whereby increased competition from foreign companies forces less efficient domestic companies to exit and more efficient ones to innovate and raises the efficiency of the overall national economy.
2. A scale effect that allows producers to more fully exploit economies of scale by selling to a larger market.
3. A backwardness effect arising from less advanced countries or sectors of an economy catching up with the more advanced countries or sectors through knowledge spillovers.

Open trade also affects the innovation process by encouraging higher levels of spending on R&D and on human capital as companies invest to take advantage of access to larger markets and the greater flow of ideas and knowledge among countries. The rate of return to new investment increases, as does the rate of economic growth. In general, most countries gain from open trade, with the scale effect benefiting smaller countries and the backwardness effect benefiting the poorer, less developed countries. But trade can also retard growth in some cases, especially in small countries that lag behind the technology leaders. Opening these countries to trade may discourage domestic innovation because companies will recognize that, even if they innovate, they may lose out to more efficient foreign companies.

Although both the neoclassical and the endogenous models of growth show the benefits of open markets, over the last 50 years developing countries have pursued two contrasting strategies for economic development:

Inward-oriented policies attempt to develop domestic industries by restricting imports. Instead of importing goods and services, these policies encourage the production of domestic substitutes, despite the fact that it may be more costly to do so. These policies are also called import substitution policies.
Outward-oriented policies attempt to integrate domestic industries with those of the global economy through trade and make exports a key driver of growth.

Many African and Latin American countries pursued inward-oriented policies from the 1950s to the 1980s that resulted in poor GDP growth and inefficient industries producing low-quality goods. In contrast, many East Asian countries, such as Singapore and South Korea, pursued outward-oriented polices during this same period, which resulted in high rates of GDP growth and convergence with developed countries. These countries also benefited from the positive effects of foreign direct investment, which suggests that more open and trade-oriented economies will grow at a faster rate. The evidence strongly supports this case.

Learning Module 3: Economics of Regulation

Describe the economic rationale for regulatory intervention
Explain the purposes of regulating commerce and financial markets
Describe anticompetitive behaviors targeted by antitrust laws globally and evaluate the antitrust risk associated with a given business strategy
Describe classifications of regulations and regulators
Describe uses of self-regulation in financial markets
Describe regulatory interdependencies and their effects describe tools of regulatory intervention in markets
Describe benefits and costs of regulation
Describe the considerations when evaluating the effects of regulation on an industry

Regulation can be described as a form of government intervention in markets that involves rules and their enforcement.

Economic rationale for regulatory

3.1 Describe the economic rationale for regulatory intervention

The case for regulatory intervention rests on the presence of informational frictions, externalities, weak competition, and social objectives.
- Informational frictions are market inefficiencies that lead to sub-optimal outcomes. They include lack of access to information and inadequate information. These issues include “adverse selection” (private information in the hands of some, but not all, market participants that allows the holder of that information to gain at the expense of others) and “moral hazard” (incentive conflicts that arise from the delegation of decision making to agents or from contracts that will affect the behavior of one party to the contract to the detriment of the other party). Asymmetrical information, in general, may give one entity an inherent advantage over another entity with which interaction occurs. The resulting regulation focuses on establishing rights and responsibilities of entities and on seeking to establish a level playing field in the dissemination of information in the market.
- Externalities are spillover effects of production and consumption activities onto others who are not directly involved in a particular transaction, activity, or decision. A positive externality provides a spillover benefit, and a negative externality generates a spillover cost. E.g., neighbors may benefit from increases in their home values resulting from renovations to a nearby house.
- Weak competition can also give rise to regulatory intervention. Weak competition is considered to be detrimental to consumers owing to high prices, less choice, and lack of innovation. It is associated with scenarios in which a dominant firm has significant market power or in which firms collude and agree to keep prices high.
- Social objectives are typically resolved by the provision of public goods that the market would not otherwise provide. An important feature of public goods is that consumption by one individual does not reduce the availability of the good for others. Usually funded by the government, public goods include defense, police protection, and education.
The regulation of securities markets and financial institutions is essential because of the consequences to society of failures in the financial system. These rules oriented toward transparency, equitable access to information (which, in turn, encourages capital formation), and protecting small investors implicitly serve to promote confidence in the markets.
- Among the objectives of many financial regulators is the protection of consumers and investors, the safety and soundness of financial institutions, the smooth operation of payment systems, and access to credit.
- Other (macroeconomic) concerns of financial regulators, particularly central banks, include price stability, levels of employment/ unemployment, and economic growth.
- A key focus of regulators is maintaining the integrity of markets, ensuring that they operate efficiently and that consumers and investors are informed and not exploited.
- Many of the regulations governing securities markets are designed to mitigate agency problems that arise through delegation to intermediaries. (Disclosure)
Prudential supervision is regulation and monitoring of the safety and soundness of financial institutions in order to promote financial stability, reduce system-wide risks, and protect customers of financial institutions.
- Types of prudential supervision include those that focus on diversifying assets, managing and monitoring risk taking, and ensuring adequate capitalization.
The benefits of regulation, however, generally come with associated costs.

Regulating of commerce

3.2 Explain the purposes of regulating commerce and financial markets

Local environmental issue, global environmental issue need international mechanisms to facilitate the coordination and acceptance of responsibilities among national governments
Trade agreements are important to global commerce. At the national, regional, or local level, governments can facilitate basic features of the business environment, such as establishing the legal framework for contracting and setting standards.
Regulation is also central to fundamental aspects of labor markets, such as workers’ and employers’ rights and responsibilities, as well as workplace safety.
Immigration issues are also handled through regulation.
Fundamental safety regulations with respect to drugs, food products, medical devices, and pollution are significant too.
Government policies regulate intellectual property, prescribing standards and processes that define and govern patents, trademarks, and copyrights.
New regulations, such as the General Data Protection Regulation (GDPR) and the proposed e-Privacy Regulation in the European Union, require entities, including businesses and governments, to apply certain protections and safeguards to personal data in their possession and maintain appropriate security procedures.
Clearly defined rules governing contracts, their interpretation, and each party’s legal rights under a contract are necessary.

Antitrust regulation and framework

3.3 Describe anticompetitive behaviors targeted by antitrust laws globally and evaluate the antitrust risk associated with a given business strategy

Anticompetitive behaviors:

Mergers that substantially lessen competition
Exclusive dealings and refusals to deal
Price discrimination
Engaging in predatory pricing

Antitrust risk associated with a given business strategy:

Increasing focus on applying antitrust laws to the technology sector.
In Europe, for example, Google was found to have abused its dominant position in the internet search market by favoring its own comparison shopping service over those of its rivals.
Similarly, Intel was found to have abused its dominant position by engaging in exclusive dealing with certain computer equipment manufacturers and retailers.
Both companies challenged the claims on the basis that they have brought considerable benefits to consumers in terms of low prices and ever-improving quality.
Using competition laws to challenge rivals can also represent a business strategy. An example of such a challenge is Microsoft’s challenge in Europe that Google is unfairly impeding competition in the search engine market.

A significant issue that companies need to face in addressing antitrust (lack of competition) issues is that in many cases, they need to satisfy simultaneously a range of regulators across multiple jurisdictions.

Classifications of regulations and regulators

3.4 Describe classifications of regulations and regulators

Broadly speaking, regulators can be either sanctioned by the government or created by an industry on a voluntary basis.
Government-backed regulatory bodies can be either governmental departments and agencies or independent regulators, which derive their power and authority from the state
A legislative body enacts a statute at a broad level, leaving it to regulatory bodies to implement and apply the detail of the regulation. State-backed regulations can, therefore, be classified as comprising
- laws enacted by legislative bodies (statutes)
- rules issued by government agencies or other regulators (administrative regulations or administrative law)
- interpretations of courts (judicial law)
Although government departments and agencies make many regulations, independent regulators can also make regulations in accordance with their powers and objectives.

3.5 Describe uses of self-regulation in financial markets

In contrast to state-backed government agencies or independent regulators, industry self-regulatory bodies are private organizations that both represent and regulate their members.
- This authority does not have the force of law, but industry self-regulatory bodies do have the power to exclude or expel parties from being members.
- To ensure minimum standards are maintained, certain entry requirements (such as training or ethical standards) may be imposed.
Some industry self-regulatory bodies, particularly in the securities industry, are known as self-regulating organizations (SROs).
SROs differ from standard industry self-regulatory bodies in that they are given recognition and authority, including enforcement power, by a government body or agency.
SROs are funded independently, rather than by the government. For example, the US SEC, the government agency that regulates the securities markets in the United States, allocates some regulatory responsibilities to the Financial Industry Regulatory Authority (FINRA), which is an SRO. It has the authority to enforce industry rules and federal securities laws. They typically regulate behaviors and often provide public goods in the form of standards.
The role of SROs varies among countries. In some countries, such as the United States, SROs have specific regulatory authority, and in other countries, self-regulating organizations are rarely or never recognized as independent regulators.

Although much of the focus of this reading is on the rules themselves and their development, impact, and implementation, regulatory enforcement and sanctions also play an important role. This division between development and enforcement of regulation also represents a possible way to classify laws or regulation. Substantive law focuses on the rights and responsibilities of entities and relationships among entities, and procedural law focuses on the protection and enforcement of the substantive laws. Regulators typically have responsibility for both substantive and procedural aspects of their regulations.

Regulatory interdependencies

3.6 Describe regulatory interdependencies and their effects

Academics have argued that regulation can sometimes enhance and work to the benefit of the interests of the regulated. This argument is often called the “regulatory capture” theory (see Stigler 1971). For example, regulatory actions and determinations can restrict potential competition (for example, by limiting entry) or effectively coordinate the choices of rivals (by imposing certain quality standards or price controls).

Regulatory differences across jurisdictions can lead to shifts in location and behavior of entities because of regulatory competition and regulatory arbitrage. Regulators may compete to provide a regulatory environment designed to attract certain entities (regulatory competition). As a result, companies may engage in regulatory arbitrage.

Interdependence in the actions of regulators dealing with the same issues and activities is important in the international arena. Such issues as financial systemic risk, terrorism financing, money laundering, and climate change reflect global concerns and, therefore, are well suited to an approach based on regulatory cooperation and coordination.

For other issues, however, domestic regulators in specific jurisdictions often adopt different perspectives or face different trade-offs when developing and applying regulations in their jurisdiction. These varying perspectives can lead to differences in regulatory treatments of the same issue across countries.

Bank supervisors (whether as a function of the central bank, another entity, or a combination of entities) generally focus on prudential supervision—regulation and monitoring of the safety and soundness of financial institutions in order to promote financial stability, reduce system-wide risks, and protect customers of financial institutions.

The objectives of securities commissions or regulators are typically to protect investors; ensure that markets are fair, efficient, and transparent; and reduce systemic risk.

In some situations, the goals of the bank supervisor and securities regulator can be in tension, resulting in conflicting objectives. A general conclusion is that regulation by different regulators, even with seemingly similar objectives, can lead to very different regulatory outcomes.

Regulatory tools

3.7 Describe tools of regulatory intervention in markets

Regulatory tools and government interventions in markets include the use of price mechanisms, such as taxes and subsidies; regulatory mandates and restrictions on behaviors, including establishing rights and responsibilities; provision of public goods; and public financing of private projects.

Use of price mechanisms

the use of a price mechanism is to create the appropriate marginal incentives and an efficient allocation of resources
taxes and subsidies: For example, By taxing polluters (or subsidizing those who do not pollute, by using a suitable baseline), one can create a system in which marginal incentives are equated across economic agents.

Regulatory mandates and restrictions on behaviors,

Governments can intervene in markets in ways other than through the price mechanism. These include

Restricting some activities (e.g., insider trading and short selling)
Mandating some activities (e.g., capital requirements for banks and registration with a securities commission for certain activities)
Providing public goods (e.g., national defense and transportation infrastructure)
Financing private projects (e.g., loans to individuals or companies for specified activities that the government deems desirable to encourage)

The extent of government provision of public goods and government financing of private projects depends on a number of factors, including the political philosophy of the country and/or government in power, the structure of the government, and the country’s gross domestic product.

The problem of systemic risk (the risk of failure of the financial system) as a result of the failure of a major financial institution has emerged as an issue in many countries around the world in the aftermath of the 2008 global financial crisis. Systemic risk and financial contagion (a situation in which financial shocks spread from their place of origin to other regions; in essence, a faltering economy infects other, healthier economies) are examples of negative externalities.

Cost–Benefit Analysis

3.8 Describe benefits and costs of regulation

In assessing regulation and regulatory outcomes, it is common practice for regulators to assess the overall benefits and costs of regulatory proposals to assess the trade-offs associated with a particular regulatory action and to assess alternative solutions. Regulators, guided by economic principles, strive to develop techniques to enhance the measurement of the costs and benefits of regulations.

Many regulators focus narrowly on the implementation costs of regulation (for example, how many compliance lawyers will need to be hired—and at what cost),
but in many instances, the most significant costs are the indirect costs that relate to the ways in which economic decisions and behavior are altered and market allocations are changed. Regulators view some of the costs associated with regulations as “unintended,” but it is important to distinguish between two types of such costs. There may be implementation costs that were unanticipated (for example, if it turns out more compliance lawyers need to be hired than originally thought) and indirect costs because of unintended consequences.

Regulatory burden refers to the costs of regulation for the regulated entity; these costs are sometimes viewed as the private costs of regulation or government burden. Net regulatory burden is the private costs of regulation less the private benefits of regulation.

Regulatory costs and benefits are especially difficult to assess on a prospective basis relative to a retrospective basis. An after-the-fact analysis (or on a retrospective) allows a comparison of the item(s) of interest before and after the regulation occurs.

Analysis of regulation

3.9 Describe the considerations when evaluating the effects of regulation on an industry

Analysts need to understand not just how regulation affects companies and industries at present; they should also be able to understand and anticipate the impact of proposed new or changing regulations on the future prospects for companies and industries.

Assessment of the likelihood of regulatory change

The analyst will need to assess the likelihood of the proposed regulation actually being implemented. Understanding the regulator’s intentions, the cost–benefit analysis framework used by the regulator, and the extent of engagement with the regulated companies will help the analyst draw conclusions about the likelihood that the proposed regulation will be implemented. Where relevant, public and political pressure may also play a role in determining the likelihood that regulatory intervention will materialize.

Assessment of the impact of regulatory change on a sector

Impact on revenues
- Regulatory bodies sometimes introduce limits on prices, tariffs, rents, or fees that companies may charge, usually to protect consumers. Alternatively, certain products or services may be banned by the regulators, or companies may be required to provide product descriptions that discourage their consumption (food or tobacco product labeling). The analyst would need to estimate the impact of such regulatory interventions on the companies’ turnover, noting that not all entities in the sector would be affected equally.
- In some scenarios, pricing or charging may not be regulated or limited by the regulator in any way, but companies may be required to increase their pricing transparency and provide a detailed breakdown of their fees.
Cost impact
- Compliance with some regulations results in additional costs for companies. These costs could take the form of higher operating expenses if, for example, manufactured products need to incorporate new safety features. Alternatively, these costs could take the form of higher capital expenditure if additional or new equipment is required. Analysts may also need to consider additional costs related to minimum wages, increased information disclosure, and data protection requirements. Companies may also incur additional costs resulting from the need to use (or not to use) certain raw materials, introduce product features, or subject themselves to regular inspections that make products or services safer for consumers. There may be costs related to expensive wastewater treatment for certain industries. The analyst will try to estimate such costs and incorporate their impact into forecasts of a company’s future profitability.
Business risk
- Many industries have seen greater regulator involvement in the form of fines, requirements to pay compensation to customers, or bans on certain activities. Such events are difficult to forecast, and their impact may be hard to quantify and incorporate into future cash flow or growth forecasts.